A extra dimension in triangulation Deaunay II / Una dimensión más en la triangulación de Deaunay II

Continúa de: http://carreteras-laser-escaner.blogspot.com/2014/11/a-extra-dimension-in-triangulation.html
Continued from: http://carreteras-laser-escaner.blogspot.com/2014/11/a-extra-dimension-in-triangulation.html

CÍRCULOS MÁXIMOS / MAXIMUS CIRCLES

Ahora vamos a ponernos a buscar un método que pueda buscar todos los triángulos (o al menos casi todos)

Now let's get to find a method that can find all the triangles (or at least most)

Tomados tres puntos, se haya la circunferencia que pasa por ellos (en 3D) y se evalúa si el resto de puntos está fuera (como el azul) o dentro (como el amarillo o el verde). Si todos están fuera se acepta el triángulo. En caso contrario se desestima esta terna.

La primera dificultad es la de encontrar una esfera (su radio y centro) dados tres puntos que forman su círculo máximo. La función en VB es la siguiente: (con un poco de orden se puede traducir a cualquier otro lenguaje:


Taken three points, the circle through them (in 3D) and it is evaluated whether the other points are outside (like blue) or inside (such as yellow or green) _. If everyone is out, the triangle is accepted. Otherwise this trio is dismissed. 

The first difficulty is to find a sphere (its radius and center) given three points that form the circle. The function in VB is: (with a bit of order can be translated into any other language:


Sub RCcon3P(_
   byVal a As Double, byVal b As Double, byVal c As Double, _
   byVal d As Double, byVal e As Double, byVal f As Double, _
   byVal g As Double, byVal h As Double, byVal i As Double)
    j=Sqr(((a-d)^2)+((b-e)^2)+((c-f)^2))
    k=Sqr(((d-g)^2)+((e-h)^2)+((f-i)^2))
    l=Sqr(((a-g)^2)+((b-h)^2)+((c-i)^2))
    ji=(d-a)/j: jj=(e-b)/j: jk=(f-c)/j
    li=(g-a)/l: lj=(h-b)/l: lk=(i-c)/l
    co=(j^2+l^2-k^2)/2/j/l): n = co*l
    m=Sqr(l^2-n^2)
    p=a+n*ji: q=b+n*jj: s=c+n*jk
    mi=(g-p)/m: mj=(h-q)/m: mk=(i-s)/m
    se=Sqr(1-co^2): R=k/se/2
    x=j/2: y=Sqr(R^2-x^2)

    CentroX = a+(x*ji)+(y*mi)
    CentroY = b+(x*jj)+(y*mj)
    CentroZ = c+(x*jk)+(y*mk)
    Radio=R
End Sub

NOTA:
Las variables CentroX,Y,Z y Radio son globales para que el dato salga de la subrutina
Si está puesta la Option Explicit hay que crar las variables que se usan, de tipo Double.

El resultado es el siguiente:


NOTE:
Centrox variables, Y, Z and Radio are global for the data leaves the subroutine 
If you set the Option Explicit must create the variables used. They are type Double. 

The result is as follows:

Otra vista:
Other saw:

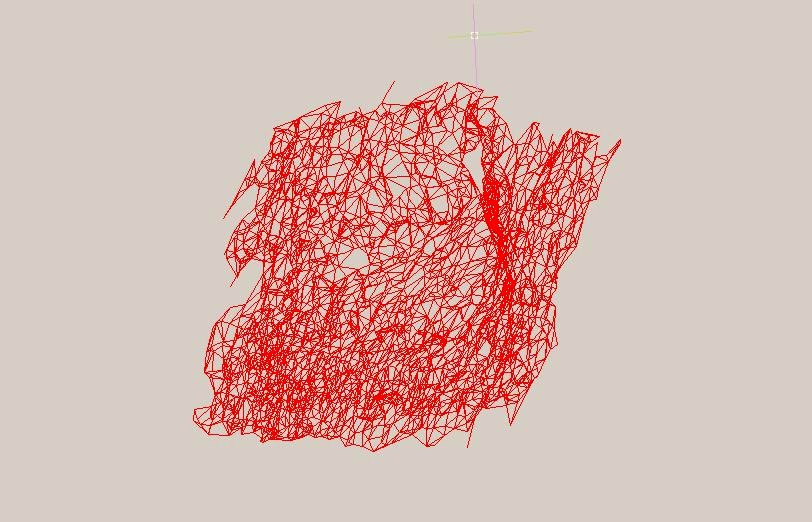
La triangulación es casi completa. Mucho menos rápida ya que evalúa una terna con el resto de puntos (max⁴ operaciones). Quedan huecos porque, entre otras cosas para no eternizarnos le hemos dicho al programa que si los puntos no estaban a un mínimo de distancia ni intentara el cálculo. Esto ha reducido el tiempo, pero ha bajado un poco la calidad.

Triangulation is almost complete. Much less rapid and evaluating a short list with the remaining points (max⁴ operations). Are hollow because, among other things not eternizarnos we told the program that if the points were not at least try to distance or calculation. This has reduced the time, but a bit lower quality.

UN EJEMPLO MÁS COMPLEJO:

Hemos conseguido un archivo de nuestra web gestora de archivos .las: http://sitegi.enmacosa.com, Particularmente de la carretera OU-536, pk 28+260:

Y hemos descargado el archivo .las correspondiente con las siguientes características:

Vemos que el número de puntos que contiene es de 14.701.745. Está claro que no tenemos un ordenador que nos permita triangular tan ingente cantidad de puntos. Reducir el número de puntos y que éstos sean relevantes es una tarea muy importante.

El primer filtro será leer sólo un porcentaje. El segundo será eliminar los puntos que sean más cercanos a una distancia dada. Por último el tercer filtro será no incluir en la búsqueda de putos potenciales de formar triángulos los más alejados a una distancia dada.

Cuando se escogen 1 de cada 1000 la cifra de puntos se reduce a 14.701 y si se eliminan los puntos más cercanos a 0.05 m, el número de puntos se reduce a 12275. Se toma como lejanía máxima, 2 metros.  El resultado de la triangulación sería: 

Si se quiere ver cómo se forma os dejo este vídeo:

Otra solución con 1 de cada 100, cercanía mínima 0.25 y lejanía máxima 5. La primera reducción es hasta los 14.701  puntos, la segunda es hasta los 4.936. El resultado es éste:

DELAUNAY CON ESFERAS / DELAUNAY WITH SPHERES

Otra posibilidad es la de hacer no una triangulación con círculo sino una tetraelización con esferas. La tretraedrización, la obtención de cuaternas de puntos de una colección de puntos en la que ponemos la condición de que no tenga ningún otro punto de la colección dentro de la esfera definida.

El primer paso sería la obtención del centro y radio de la esfera que pasa por cuatro puntos. Definimos la subrutina:


Another possibility is to make no triangulation circle but tetrahedrons with spheres. Obtaining quadruples of points of a collection of points on the condition that we do not have any other point of collection within the defined area. 

The first step would be to obtain the center and radius of the sphere passing through four points. We define the subroutine:

Sub Esfera(

   byVal a As Single, byVal b As Single, byVal c As Single,_

   byVal d As Single, byVal e As Single, byVal f As Single,_

   byVal g As Single, byVal h As Single, byVal i As Single,_

   byVal j As Single, byVal k As Single, byVal l As Single)

km E(5, 5) As Single

km r As Single

E(1,1)=a: E(2,1)=b: E(3,1)= c: E(4,1) = 1

E(1,2)=d: E(2,2)=e: E(3,2)= f: E(4,2) = 1

E(1,3)=g: E(2,3)=h: E(3,3)= i: E(4,3) = 1

E(1,4)=j: E(2,4)=k: E(3,4)= l: E(4,4) = 1

ello=Det(E,4,r): M11=r

E(1,1)=a^2+b^2+c^2: E(2,1)=b: E(3,1)=c: E(4,1)=1

E(1,2)=d^2+e^2+f^2: E(2,2)=e: E(3,2)=f: E(4,2)=1

E(1,3)=g^2+h^2+i^2: E(2,3)=h: E(3,3)=i: E(4,3)=1

E(1,4)=j^2+k^2+l^2: E(2,4)=k: E(3,4)=l: E(4,4)=1

ello=Det(E,4,r): M12=r

E(1,1)=a^2+b^2+c^2: E(2,1)=a: E(3,1)=c: E(4,1)=1

E(1,2)=d^2+e^2+f^2: E(2,2)=d: E(3,2)=f: E(4,2)=1

E(1,3)=g^2+h^2+i^2: E(2,3)=g: E(3,3)=i: E(4,3)=1

E(1,4)=j^2+k^2+l^2: E(2,4)=j: E(3,4)=l: E(4,4)=1

ello=Det(E,4,r): M13=r

E(1,1)=a^2+b^2+c^2: E(2,1)=a: E(3,1)=b: E(4,1)=1

E(1,2)=d^2+e^2+f^2: E(2,2)=d: E(3,2)=e: E(4,2)=1

E(1,3)=g^2+h^2+i^2: E(2,3)=g: E(3,3)=h: E(4,3)=1

E(1,4)=j^2+k^2+l^2: E(2,4)=j: E(3,4)=k: E(4,4)=1

ello=Det(E,4,r): M14=r

E(1,1)=a^2+b^2+c^2: E(2,1)=a: E(3,1)=c: E(4,1)=c

E(1,2)=d^2+e^2+f^2: E(2,2)=d: E(3,2)=f: E(4,2)=f

E(1,3)=g^2+h^2+i^2: E(2,3)=g: E(3,3)=i: E(4,3)=i

E(1,4)=j^2+k^2+l^2: E(2,4)=j: E(3,4)=l: E(4,4)=l

ello=Det(E,4,r): M15=r

CentroX= 0.5*M12/M11

CentroY=-0.5*M13/M11

CentroZ= 0.5*M14/M11

Radio=(a-CenX)^2+(b-CenY)^2+(c-CenZ)^2

End Sub

Hace falta la función de resolución de determinantes:
The determinants resolution function is required:

Function Det(ByRef Matrix() As Single, Norder As Integer, deter As Single)
Dim k,k1,i,j As Integer
Dim save As Single
Dim check As Boolean
deter=1
For k=1 To Norder
  If Matrix(k,k)=0 Then
  j=k
  Do
    check=True:
    If Matrix(k,j)=0 Then
        If j=Norder Then det=0: Exit Function
        check=False: j=j+1
      End If
      If Matrix(k,j)<>0 Then
        For i=k To Norder
           save=Matrix(i,j)
           Matrix(i,j)=Matrix(i,k)
           Matrix(i,k)=save
        Nexti
        deter=-deter
      End If
    Loop While check=False
    End If
    deter=deter*Matrix(k,k)
    If k-Norder<0 Then
    k1=k+1
    For i= k1 To Norder: Forj=k1ToNorder
      Matrix(i,j)=Matrix(i,j)-(Matrix(i,k)*Matrix(k,j)/Matrix(k,k))
    Next j,i
  End If
Nextk
EndFunction

Y con esto ya podemos hacer el cálculo general:
And with this, we can make the general calculation:

Dada una colección de puntos [x_i, y_i, z_i], i Î {1..max}

for i=1 .. max-3

  for j=1 .. max-2

    for k=1 .. max-1

      for l=1 .. max

         Se halla la esfera → R,  [Cx_i, Cy_i, Cz_i]

            for n=1 .. max (sin i, ni j, ni k, ni l)

           Se compueba que  [x_n, y_n, z_n] Ï {R,  [Cx_i, Cy_i, Cz_i]}  

           →  se guarda la cuaterna [i, j, k, l] 

              como cuaterna de índices del tetraedro obtenido.

El proceso hace, aproximadamente, max⁵ operaciones. Con  4.000 puntos el número de operaciones dentro del bucle sería de 1.024.000.000.000.000.000 operaciones. No sólo es brutal sino que además queda después el trabajo de depurar de las cuatro caras del tetraedro, dentro de las ocho posibles, los dos triángulos correctos.

He hecho pruebas que ni muestro porque como tardan una exageración si muestro el trabajo a medio hacer son feas y si lo muestro hecho no acabo en un año.

The process makes about  max⁵ operations. With 4000 points the number of operations within the loop would 1,024,000,000,000,000,000 operations. It is not only brutal but also left after purifying work of the four faces of the tetrahedron, within eight possible, the two right triangles. 

I have done tests that show because as slow or exaggeration to show the job half done are ugly and if I do not I just show you made ​​in a year.