Artículo patrocinado por Enmacosa dentro del proyecto "Formigón estructural", cofinanciado por la Xunta de Galicia (2013).
Autores: Alba Catoira, Juan Luis Pérez, Juan R. Rabuñal y Fernando Martínez-AbellaResumen
El objetivo principal que se presenta en este artículo es mostrar las virtudes del empleo de la Programación Genética (GP) como herramienta en la extracción de conocimiento de datos experimentales. El ejemplo elegido para ello se enmarca dentro del ámbito de la Ingeniería Civil.
Se presenta pues, un sistema de Programación Genética Distribuida que aplica un algoritmo de clustering para alcanzar soluciones más heterogéneas. La finalidad del sistema es la de extraer fórmulas matemáticas (regresión simbólica) a través de un conjunto de datos de entrada y sus correspondientes salidas utilizando para ello una versión distribuida del método de Programación Genética clásico. La distribución del algoritmo permite disminuir considerablemente el número de pruebas necesarias para alcanzar una solución óptima, disminuyendo a su vez el coste humano y de recursos asociado.
I. INTRODUCCIÓN
En el ámbito de la Ingeniería Civil, al igual que en otras disciplinas, se requiere predecir el comportamiento de determinados materiales o estructuras en función de diversas condiciones de contorno que influyen su comportamiento teórico. Es aquí, tras la experiencia adquirida en los ensayos de laboratorio y materializada en conjuntos de datos que relacionan entradas con salidas reales, donde la Programación Genética (PG) [1] resulta de gran utilidad puesto que permite realizar regresión simbólica sobre un conjunto de datos experimentales. La PG es una técnica de búsqueda inherentemente paralela que requiere gran cantidad de cálculos complejos. Dicha complejidad hace que la distribución de los cálculos sea de gran utilidad.
Es por ello que se ha propuesto que el sistema desarrollado sea distribuido, permitiendo así reducir el tiempo de cálculo. En este contexto, cuando el espacio de búsqueda es amplio y complejo, es común obtener procesos evolutivos que lleven a mínimos locales. Por este motivo, en este trabajo se utiliza una ejecución paralela del algoritmo mediante varias poblaciones que intercambian individuos entre ellas, aumentando la heterogeneidad.
El sistema desarrollado denominado “DistClustPG” [2] aplica un algoritmo de clustering [3] [4] para dividir cada población en grupos de acuerdo a una medida de similitud. A continuación, se eligen los representantes de cada grupo para formar parte del proceso de migración entre poblaciones consiguiendo así, además de la distribución del cómputo, una estrategia co-evolutiva.
II. SISTEMA DISTRIBUIDO DE PROGRAMACIÓN GENÉTICA
El DistClustPG está basado en la ejecución paralela del algoritmo de PG sobre poblaciones independientes o porciones de una sola población. Cada población evoluciona localmente mediante el algoritmo PG de forma independiente, y contribuye a la evolución total del sistema a través de un intercambio periódico de individuos.
En la PG clásica puede ocurrir que un individuo (fórmula matemática) tenga un valor de fitness óptimo y, sin embargo, que su estructura sea demasiado compleja para la posterior interpretación por parte de los expertos (en este caso en Ingeniería Civil), o bien que dos individuos con el mismo valor de fitness sean estructuralmente muy diferentes. Es por ello que tras un número de generaciones previamente establecido por el experto, cada nodo aplica el algoritmo de clustering sobre su población, dividiéndola en grupos según una medida de similitud. Dicha medida de similitud mide la distancia entre un individuo (representado en forma de árbol) y el árbol vacío. De este modo, se crean grupos según el nivel de complejidad estructural de los individuos. Una vez creados los grupos, se elige a los representantes de los mismos (el de mejor valor de fitness) y estos representantes son los que forman parte del proceso de migración.
Cada nodo envía sus representantes al nodo maestro, que a su vez, los incorpora a su propia población, y aplica el algoritmo de PG sobre ellos, haciéndolos evolucionar. Tras un número de generaciones preestablecido, el nodo maestro aplica su algoritmo de clustering sobre la población evolucionada, y envía sus representantes a todos los nodos del sistema.
A. Arquitectura de DistClustPG
El entorno básico en el que se utiliza el sistema es una red Ethernet de ordenadores. DistClustPG está constituido por un nodo maestro y una serie de nodos denominados esclavos, de acuerdo con el esquema de arquitectura típico maestro-esclavo. El nodo principal o maestro es el que gestiona la ejecución de los nodos esclavos y almacena los resultados obtenidos en los mismos. Es también el responsable de enviar a los demás nodos las órdenes y los datos necesarios para la ejecución (parámetros, patrones, etc.). Los esclavos poseen el algoritmo PG y el algoritmo de clustering para poder evolucionar su población.
Tras un número prefijado de generaciones, los nodos aplicarán el algoritmo de clustering, agrupando a los individuos de la población actual en grupos de acuerdo a una medida de similitud. Posteriormente, eligen a los representantes de cada grupo y se los envían al nodo maestro, que posee su propia copia del algoritmo PG y de clustering, y que hará evolucionar a su vez los individuos recibidos de los esclavos. En todo este proceso anteriormente descrito, los nodos sólo detienen su ejecución de PG para aplicar el algoritmo de clustering. Es entonces cuando incorporan a su población aquellos individuos que han recibido de otros nodos (almacenados temporalmente en un buffer). De este modo, se obtiene un mayor rendimiento. La Figura 1 muestra el diagrama de secuencia del funcionamiento de la arquitectura DistClustPG.
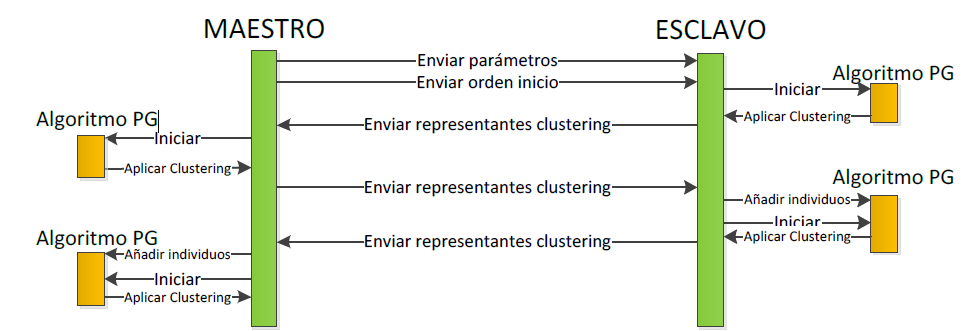 |
| Fig. 1. Diagrama de secuencia |
Donde d(R1,R2) = | key(R1)-key(R2)|, y key es una función de codificación que asigna un valor numérico a cada nodo en el árbol según su tipo, childi(Y) es el iésimo hijo de los m posibles del nodo Y si i≤m o el árbol vacío en otro caso. La constante K se usa para dar diferentes pesos a los nodos según su nivel de profundidad en el árbol. En caso de calcular la distancia entre un árbol y el árbol vacío, el resultado sería la suma de las claves del árbol ponderadas por su nivel de profundidad.
Supongamos el siguiente árbol (representado en la Figura 2):
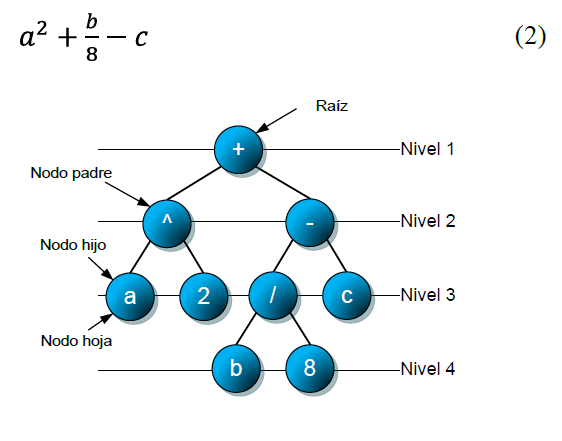 |
| Fig. 2. Un ejemplo de árbol. |
En la siguiente tabla, se muestran los valores asociados a cada uno de los nodos. Estos valores han sido establecidos mediante experimentación, y de forma que las claves entre operadores de un mismo grupo sean más similares que entre grupos.
 |
| TABLA I CLAVES DE LOS OPERADORES |
La distancia entre el árbol anterior y el árbol vacío vendría determinada por la ecuación (3).
Los individuos de la población son ordenados en base a la distancia al árbol vacío, y se crean grupos teniendo en cuenta un valor umbral, que se recalcula en cada ejecución del algoritmo. El experto establece el máximo porcentaje de clusters que desea crear en función del tamaño de la población y el umbral se calcula como se muestra en la ecuación (4).
donde dmax y dmin son la máxima y mínima distancia al árbol vacío en la población, respectivamente, y max número de clusters desscrita en la ecuación (5).
Para crear los clusters, se toma como referencia el primer individuo de la población ordenada, y estarán en el mismo grupo aquellos individuos cuyas distancias al árbol vacío no superen el umbral. Si esta condición no se cumple para un individuo, éste se convierte en el nuevo elemento de referencia y se crea un nuevo grupo.
Una vez se hayan clasificado todos los individuos, se ordena internamente cada grupo según el valor de ajuste, y se elige al de mejor fitness como representante. Si el resultado del proceso de clustering fue la creación de k clusters, habrá k representantes, que se enviarán al nodo maestro para formar parte de su población.
Al igual que los esclavos, el nodo maestro aplicara el algoritmo PG sobre los individuos recibidos, aplicará el algoritmo de clustering y enviará a los esclavos sus propios representantes.
III. RESULTADOS EXPERIMENTALES
El hormigón de altas prestaciones (HPC: High-Performance Concrete) constituye una evolución muy empleada en la industria de la construcción con hormigón. Además de los tres componentes básicos del hormigón convencional, que son el cemento, los áridos (finos y gruesos) y el agua, la elaboración de HPC incorpora adiciones como cenizas volantes (fly ash), escoria del horno (blast fumace slag) y aditivos químicos como fluidificantes, aceleradores y retardadores de fraguado…[9] [10]. El HPC es un material altamente complejo, lo que implica que conocer a priori el comportamiento del hormigón dados los materiales empleados resulta una tarea no resuelta.
El índice de Abrams o la relación agua-cemento (w/c) conocido en 1918 [11] Constituye, junto a la cantidad de cemento, el índice más significativo de la mezcla de hormigón ya que se encuentra en relación inversamente proporcional a la resistencia del hormigón [12]. La relación a/c y la cantidad de cemento determinan, pues, junto al resto de componentes, la resistencia final que presentará una muestra de hormigón. En la actualidad no existe una formulación ni analítica ni empírica que prediga la resistencia del hormigón a partir de sus componentes, a pesar de la existencia de series de datos extensas. Contar con ella, sin lugar a dudas, supondría un importante avance en el conocimiento [13].
Una vez presentado el problema, se detallan las soluciones al mismo comparando los resultados de la aproximación clásica de Programación Genética con el nuevo sistema desarrollado de Programación Genética distribuida. Por otro lado, se compara el resultado del sistema distribuido con otras aproximaciones [14], [15].
El conjunto de datos utilizado se ha obtenido de la base de datos del UCI Learning Repository [16]. El problema consta de 8 variables de entradas de tipo real: cemento(c), el agua (w), la escoria (sl), la ceniza volante (fl), el superplastificante (sp), el árido grueso (ca), el árido fino (fa) y la edad de ensayo (age). Se han empleado 720 patrones de entrada para la fase de entrenamiento y 308 patrones para la fase de test. En la Tabla 2 pueden verse los rangos de valores típicos para las variables que utilizarán ambos sistemas. La salida es la resistencia del hormigón a la compresión, de la que se pretende conseguir una expresión matemática que modele el comportamiento real para el caso del HAP.
A. Comparación con la PG clásica
Continúa en: http://carreteras-laser-escaner.blogspot.com/2014/12/regresion-simbolica-en-ingenieria-civil.html
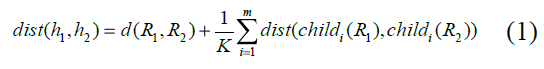


No hay comentarios:
Publicar un comentario