Artículo patrocinado por Enmacosa dentro del proyecto "Formigón estructural", cofinanciado por la Xunta de Galicia (2013).
Article sponsored by Enmacosa inside the "Formigón estructural" project, cofinanced by the Xunta de Galicia. (2013)
Adherencia y Anclaje de acero de refuerzo en Hormigón Estructural / Bond and Anchorage of Reinforcing Steel in Structural Concrete
Continue from: http://carreteras-laser-escaner.blogspot.com/2014/11/genetic-programming-to-improvement-fib.html
The method followed is oriented to improving the FIB equations developed for predicting the stress of bar anchored. The method used follows the same guidelines referred to in the paper developed by Pérez et al [7]. In summary, the method is based on GP techniques, imposing some restrictions based on knowledge of the problem provided by an expert. Symbolic regression data is one of the capabilities provided by the GP.
3 Método / Method
El método seguido se orienta a la mejora de las ecuaciones FIB desarrollados para la predicción de la tensión de la barra de anclado. El método utilizado sigue las mismas directrices mencionadas en el documento elaborado por Pérez [7]. En resumen, el método se basa en técnicas de GP imponiendo algunas restricciones basadas en el conocimiento del problema proporcionadas por un experto. Los datos de regresión simbólica son una de las capacidades proporcionadas por el GP..
The method followed is oriented to improving the FIB equations developed for predicting the stress of bar anchored. The method used follows the same guidelines referred to in the paper developed by Pérez et al [7]. In summary, the method is based on GP techniques, imposing some restrictions based on knowledge of the problem provided by an expert. Symbolic regression data is one of the capabilities provided by the GP.
Disponiendo de un conjunto de datos (input-output), el GP es capaz de relacionar estos datos con una ecuación algebraica. Su complejidad puede variar, y la integridad dimensional no está garantizada. Esta técnica, aplicada en muchos casos en ingeniería civil, es uno de los seguidos por Ashour [8], por ejemplo, para predecir la resistencia a la cortante en vigas de hormigón. Naturalmente, la forma de las ecuaciones obtenidas es muy diferente de las de los códigos comunes. El método presentado mejora los términos aceptados por la comunidad científica, conseguir un mejor ajuste cuando los resultados se aplican a una base de datos.
Having a data set (input-output), the GP is able to relate these data algebraically by an equation. Its complexity may vary, and dimensional integrity is not guaranteed. This technique, applied in many cases in civil engineering, is one of those followed by Ashour al [8], for example, to predict shear strength in concrete beams. Naturally, the form of the equations obtained is very different from the ones in the common codes. The presented method improves the terms accepted by the scientific community, getting a better fit when the results are applied to a database.
Having a data set (input-output), the GP is able to relate these data algebraically by an equation. Its complexity may vary, and dimensional integrity is not guaranteed. This technique, applied in many cases in civil engineering, is one of those followed by Ashour al [8], for example, to predict shear strength in concrete beams. Naturally, the form of the equations obtained is very different from the ones in the common codes. The presented method improves the terms accepted by the scientific community, getting a better fit when the results are applied to a database.
Se parte de la expresión FIB-2006, ya que muestra mejores resultados en la base de datos. La expresión de búsqueda determinará la resistencia predicha de la probeta (Spred) al compararse con la prueba de esfuerzo real (σtest). En primer lugar, es necesario definir cómo se evaluarán los elementos individuales en la función de aptitud (ecuación 4). En esta ecuación, σtest es la tensión de barra en la rotura, α es el coeficiente de retraso, si es el número de nodos en la expresión y n es el número de casos de la base de datos. Se deben establecer los parámetros pi y lbias definidos en la ecuación 3.
Después de realizar varias pruebas, fue adoptado lbias = 1,0, y la ecuación 4 muestra el valor de pi (DP). Esta ecuación se basa en el uso de la técnica de "puntos fijos".
It starts from the expression FIB-2006, because it shows better results over the database. The search expression will determine the bar stress predicted (spred) to be compared with the real stress test (σtest). Firstly, it is necessary to define how individuals will be evaluated in the fitness function (equation 4). In this equation, σtest is the bar stress at failure, α is the parsimony coefficient, si is the number of nodes in the expression and n is the number of cases of the database. It should set the parameters pi and lbias defined in equation 3.
Después de realizar varias pruebas, fue adoptado lbias = 1,0, y la ecuación 4 muestra el valor de pi (DP). Esta ecuación se basa en el uso de la técnica de "puntos fijos".
It starts from the expression FIB-2006, because it shows better results over the database. The search expression will determine the bar stress predicted (spred) to be compared with the real stress test (σtest). Firstly, it is necessary to define how individuals will be evaluated in the fitness function (equation 4). In this equation, σtest is the bar stress at failure, α is the parsimony coefficient, si is the number of nodes in the expression and n is the number of cases of the database. It should set the parameters pi and lbias defined in equation 3.
After performing several tests, was adopted lbias = 1.0, and equation 4 shows the value of pi (DP). This equation is based on the use of the technique of "demerit points".
La técnica se adaptó para que las búsquedas "orientadas" fueran posibles, con diferentes propósitos.
La orientación se introdujo a través de imposiciones ni restricciones, que incluyen:
─ Restricción sobre el tipo de funciones que vinculan las variables
─ Selección preferida de los elementos con el más alto proporciones σtest / σpred. Desde el punto de vista estructural, es mucho más apropiado esta opción por razones de seguridad
El método utilizado se inicia con el establecimiento de un "marco" de la programación genética que hará que el proceso evolutivo tenga en cuenta las restricciones e imposiciones.
El marco se define directamente de la ecuación FIB-2006, que se divide en subexpresiones. Además, cada subexpresión está escrita para que los factores (rama) puede cambiar en el proceso de búsqueda. Las líneas de trabajo que se pueden encontrar son:
─ La optimización de los coeficientes numéricos de la ecuación. Las ramas serán valores reales
─ La introducción de una nueva sub-expresión. Esto puede ser un número real o una función (nueva rama) vinculado a una variable
Como se ha mencionado, en este tipo de modelo es muy importante que el estrés predicho es igual o mayor que el valor real.
En general, si un individuo se diferencia del valor real está penalizado durante el entrenamiento. Desde un punto de vista matemático, S valora igual a 0.5 o 1.5 debe ser penalizado por igual. Para tener en cuenta la seguridad estructural, el individuo 0.5 debe ser penalizado más que el individuo 1,5, ya que causa la inseguridad estructural (colapso).
Esto se logra mediante la técnica de puntos fijos, con lo cual se pondera el error de la expresión de acuerdo con los rangos definidos por Pérez [9]. La función de aptitud (3) muestra cómo los pesos del factor pi el error de predicción, de acuerdo con los intervalos y valores de la ecuación (4).
El método utilizado se inicia con el establecimiento de un "marco" sobre el que la programación genética hará que el proceso evolutivo, teniendo en cuenta las restricciones e imposiciones. Tal "marco" se basa en la formulación de FIB 2006, sobre la que se va a introducir nuevas variables o sus coeficientes se modificará.
En el proceso de búsqueda se ha propuesto tres ecuaciones básicas (5) (6) (7). Cada rama se designa como Bi. La Tabla 3 muestra los valores predeterminados en práctica, sobre la base de las pruebas iniciales. Los datos de entrada no se han normalizado, por lo que las expresiones se pueden utilizar directamente.
The technique was adapted for “oriented” searches were possible, with different purposes.
La orientación se introdujo a través de imposiciones ni restricciones, que incluyen:
─ Restricción sobre el tipo de funciones que vinculan las variables
─ Selección preferida de los elementos con el más alto proporciones σtest / σpred. Desde el punto de vista estructural, es mucho más apropiado esta opción por razones de seguridad
El método utilizado se inicia con el establecimiento de un "marco" de la programación genética que hará que el proceso evolutivo tenga en cuenta las restricciones e imposiciones.
El marco se define directamente de la ecuación FIB-2006, que se divide en subexpresiones. Además, cada subexpresión está escrita para que los factores (rama) puede cambiar en el proceso de búsqueda. Las líneas de trabajo que se pueden encontrar son:
─ La optimización de los coeficientes numéricos de la ecuación. Las ramas serán valores reales
─ La introducción de una nueva sub-expresión. Esto puede ser un número real o una función (nueva rama) vinculado a una variable
Como se ha mencionado, en este tipo de modelo es muy importante que el estrés predicho es igual o mayor que el valor real.
En general, si un individuo se diferencia del valor real está penalizado durante el entrenamiento. Desde un punto de vista matemático, S valora igual a 0.5 o 1.5 debe ser penalizado por igual. Para tener en cuenta la seguridad estructural, el individuo 0.5 debe ser penalizado más que el individuo 1,5, ya que causa la inseguridad estructural (colapso).
Esto se logra mediante la técnica de puntos fijos, con lo cual se pondera el error de la expresión de acuerdo con los rangos definidos por Pérez [9]. La función de aptitud (3) muestra cómo los pesos del factor pi el error de predicción, de acuerdo con los intervalos y valores de la ecuación (4).
El método utilizado se inicia con el establecimiento de un "marco" sobre el que la programación genética hará que el proceso evolutivo, teniendo en cuenta las restricciones e imposiciones. Tal "marco" se basa en la formulación de FIB 2006, sobre la que se va a introducir nuevas variables o sus coeficientes se modificará.
En el proceso de búsqueda se ha propuesto tres ecuaciones básicas (5) (6) (7). Cada rama se designa como Bi. La Tabla 3 muestra los valores predeterminados en práctica, sobre la base de las pruebas iniciales. Los datos de entrada no se han normalizado, por lo que las expresiones se pueden utilizar directamente.
The technique was adapted for “oriented” searches were possible, with different purposes.
The orientation was introduced through impositions or restrictions, which include:
─ restriction on the type of functions that link the variables
─ preferred selection of individuals with the highest ratios σtest/σpred. From the structural point of view, is much more appropriate this option for safety reasons
The method used starts with the establishment of a “framework” from wich genetic programming will make the evolutive process, taking into account the restrictions and impositions.
The framework is defined directly from the equation FIB-2006, which is divided into subexpressions. Also, each subexpression is written indicating which factor (branch) may change in the search process. The working lines can find:
─ The optimization of the numerical coefficients of the equation. The branches will be Real values
─ The introduction of a new subexpression. This can be a Real number or a function (new branch) linked to a variable
As mentioned, in this type of model is very important that the predicted stress is equal to or greater than the actual value.
In general, if an individual differs from the real value is penalized during training.
From a mathematical point of view, S values equal to 0.5 or 1.5 should be penalized equally. To take into account the structural safety, the individual 0.5 should be penalized more than the individual 1.5, as it causes structural insecurity (collapse).
This is achieved through the technique of demerit points, whereby the error of the expression is weighted according to the ranges defined by Pérez [9]. The fitness function (3) shows how the pi factor weights the prediction error, according to the intervals and values of the equation (4).
The method used starts with the establishment of a “framework” about whom genetic programming will make the evolutive process, taking into account the restrictions and impositions. Such “framework” is based on the 2006 FIB formulation, about which it will be introduced new variables or its coefficients will be modified.
In the searching process it has been proposed three basic equations (5)(6)(7). Each branch is designated as Bi. Table 3 shows the default settings implemented, based on the initial tests. The input data have not been standardized, so expressions can be used directly.
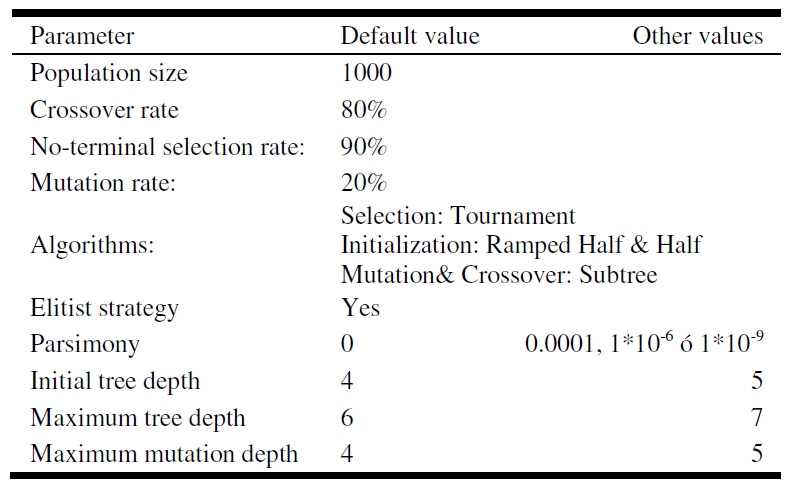 |
| Table 3. Parameters used |
Por defecto, la suma, resta, multiplicación y división protegida fueron elegidos como operadores o nodos no terminales. Las variables del conjunto de datos (ls, db, cmin, cmax y fc), y números enteros en el rango [-10, 10] fueron adoptados como los nodos terminales.
Las restricciones sobre las ecuaciones se muestran en la tabla 4. Para la ecuación (5) se han impuesto tres tipos de restricciones ("A", "B" y "C"), la restricción de "D" a la ecuación (6) y, finalmente, la restricción "se impone E "a la ecuación (7).
By default, addition, subtraction, multiplication and protected division were chosen as operators or non-terminal nodes. Variables from the data set (ls, db, cmin, cmax and fc), and integers in the range [-10, 10] were adopted as terminal nodes.
Las restricciones sobre las ecuaciones se muestran en la tabla 4. Para la ecuación (5) se han impuesto tres tipos de restricciones ("A", "B" y "C"), la restricción de "D" a la ecuación (6) y, finalmente, la restricción "se impone E "a la ecuación (7).
By default, addition, subtraction, multiplication and protected division were chosen as operators or non-terminal nodes. Variables from the data set (ls, db, cmin, cmax and fc), and integers in the range [-10, 10] were adopted as terminal nodes.
Constraints over the equations are showed in table 4. Equation (5) have three types of constraints (“A”, “B” and “C”), the constraint “D” is imposed to equation (6) and finally the constraint “E” is imposed to equation (7).
 |
| Table 4. Constraints |
4 Results
En total, más de 4.500 ejecuciones se llevaron a cabo. Los resultados se analizan fundamentalmente a través de los siguientes indicadores: COV (coeficiente de variación), σtest / σpred, R2 (raíz cuadrada de Coeficiente de correlación de Pearson), MSE (media de error de raíz cuadrada), ME (error de decir), y finalmente demérito puntos calculados según la ecuación (4).
De acuerdo con los mejores resultados, se optó por un selecto grupo de ecuaciones. Si el denominador fuera negativo, las expresiones que contienen "división protegida" fueron rechazadas. Además también se descartaron ecuaciones demasiado complejas.
PG_9RSC4 (8), PG_8v2R5 (9), PG_7v3F2 (10), PGcc6 (11) eran ecuaciones más precisas. Dado que no proporcionan mejoras sustanciales, estas ecuaciones no contienen los derivados de la GP clásico. Los resultados se muestran en la Tabla 5. La mejora significativa logrado es evidente mediante la comparación de los resultados de la FIB ecuaciones.
In total, more than 4,500 executions were carried out. The results are analyzed essentially through the following indicators: COV (variation coefficient), σtest/σpred , R2 (square root of Pearson product-moment correlation coefficient), MSE (mean square root error), ME (mean error), and finally demerit points calculated according to equation (4).
De acuerdo con los mejores resultados, se optó por un selecto grupo de ecuaciones. Si el denominador fuera negativo, las expresiones que contienen "división protegida" fueron rechazadas. Además también se descartaron ecuaciones demasiado complejas.
PG_9RSC4 (8), PG_8v2R5 (9), PG_7v3F2 (10), PGcc6 (11) eran ecuaciones más precisas. Dado que no proporcionan mejoras sustanciales, estas ecuaciones no contienen los derivados de la GP clásico. Los resultados se muestran en la Tabla 5. La mejora significativa logrado es evidente mediante la comparación de los resultados de la FIB ecuaciones.
In total, more than 4,500 executions were carried out. The results are analyzed essentially through the following indicators: COV (variation coefficient), σtest/σpred , R2 (square root of Pearson product-moment correlation coefficient), MSE (mean square root error), ME (mean error), and finally demerit points calculated according to equation (4).
According to the best results, a select group of equations was chosen. If the denominator could be negative, expressions containing function "protected division" were rejected. Also too complex equations were also discarded.
PG_9RSC4 (8), PG_8v2R5 (9), PG_7v3F2 (10), PGcc6 (11) were more accurate equations. Since not provide substantial improvements, these equations do not contain the derivatives of the classic GP. The results are shown in Table 5. The significant improvement achieved is evident by comparing the results of the equations FIB.
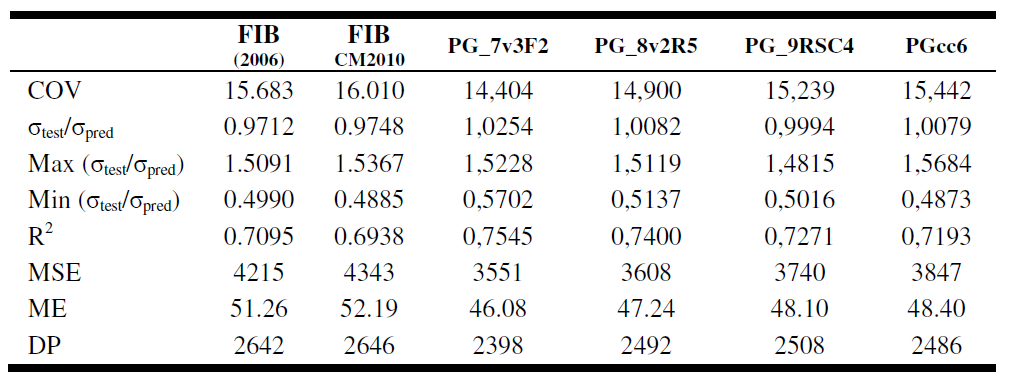 |
| Table 5. Results |
Algunas de las expresiones destacan por diferentes aspectos. PG_9RSC4 es un simple mejora de la ecuación de la FIB, logrado con mejor se ajuste de los exponentes y constantes. Para borrar el valor de la longitud, es necesario imponer condiciones a la búsqueda, que propone una primera función libre, no dependiente de la longitud, y un coeficiente de ajuste para el resto de parámetros: la ecuación PG_8v2R5 surge de esta manera. La marcada tendencia que exhibe el exponente (ls / db) al valor 0,5, induce un nuevo grupo de ejecuciones en las que se fije esta constante. Con este procedimiento, se obtiene la ecuación PG_7v3F2, lograr una distribución muy notable.
Some of the expressions stand out by different appearances. PG_9RSC4 is a simple improvement of the FIB equation, achieved with better adjusts of the exponents and constants. To clear the value of the length, it is necessary to impose conditions to the search, proposing a first free function, not dependent on the length, and a adjust coefficient for the rest of parameters: the equation PG_8v2R5 arises this way. The marked tendency that exhibits the exponent (ls/db) to the value 0.5, induces a new group of executions in which this constant is fixed. With this procedure, the PG_7v3F2 equation is obtained, achieving a very noticeable distribution.
Some of the expressions stand out by different appearances. PG_9RSC4 is a simple improvement of the FIB equation, achieved with better adjusts of the exponents and constants. To clear the value of the length, it is necessary to impose conditions to the search, proposing a first free function, not dependent on the length, and a adjust coefficient for the rest of parameters: the equation PG_8v2R5 arises this way. The marked tendency that exhibits the exponent (ls/db) to the value 0.5, induces a new group of executions in which this constant is fixed. With this procedure, the PG_7v3F2 equation is obtained, achieving a very noticeable distribution.
En los últimos grupos notables, se permite la aparición de una función libre (sin ls) que multiplica ls con exponente constante y el término clásico de la contribución de refuerzo transversal, mejorado con constantes. Esta es la expresión PGcc6, que presentan una fuerte concentración alrededor de la unidad. A continuación, las tensiones que se pueden desarrollar para algunas variables específicas se comparan en dos de las ecuaciones que se encuentran frente a las expresiones FIB deducido. Se puede observar la similitud del enfoque, incluso para ecuaciones que no nacen de la estructura de la FIB.
Como resultado de lo expuesto anteriormente, se puede recomendar para adoptar la expresión PG_7v3F2 como una buena ecuación para obtener el comportamiento de bonos de la armadura pasiva en un elemento de hormigón.
In the last remarkable groups, it is allowed the apparition of a free function (without ls) that multiplies ls with constant exponent and the classical term of transversal reinforcement contribution, improved with constants. This is the PGcc6 expression, which exhibit a strong concentration around the unit. Next, the stresses that can be developed for some specific variables are compared in two of the equations found against the FIB deduced expressions. It can be observed the similarity of the approach, even for equations that are not born from the structure of the FIB.
Como resultado de lo expuesto anteriormente, se puede recomendar para adoptar la expresión PG_7v3F2 como una buena ecuación para obtener el comportamiento de bonos de la armadura pasiva en un elemento de hormigón.
In the last remarkable groups, it is allowed the apparition of a free function (without ls) that multiplies ls with constant exponent and the classical term of transversal reinforcement contribution, improved with constants. This is the PGcc6 expression, which exhibit a strong concentration around the unit. Next, the stresses that can be developed for some specific variables are compared in two of the equations found against the FIB deduced expressions. It can be observed the similarity of the approach, even for equations that are not born from the structure of the FIB.
As a result of the previously exposed, it can be recommended to adopt the expression PG_7v3F2 as a good equation to get the bond behavior of the passive reinforcement in a concrete element.
5 Conclusions
La ecuación FIB para determinar las barras de refuerzo tensión de tracción se mejoró con la aplicación de técnicas heurísticas.
En el método aplicado, seguridad estructural se tuvo en cuenta, a través de la ponderación contemplada por puntos fijos. Como conclusión final y resumen cabe señalar que se ha logrado implementar un nuevo método basado en la programación genética para extraer conocimiento a partir de datos experimentales basados en la experiencia. Esta experiencia se implementa a través de las limitaciones que son inducidos en el algoritmo.
FIB equation to determine rebar tension stress was improved with the application of heuristic techniques.
En el método aplicado, seguridad estructural se tuvo en cuenta, a través de la ponderación contemplada por puntos fijos. Como conclusión final y resumen cabe señalar que se ha logrado implementar un nuevo método basado en la programación genética para extraer conocimiento a partir de datos experimentales basados en la experiencia. Esta experiencia se implementa a través de las limitaciones que son inducidos en el algoritmo.
FIB equation to determine rebar tension stress was improved with the application of heuristic techniques.
In the applied method, structural safety was taken into account, through the weighting provided by demerit points. As a final conclusion and summary it should be noted that it has managed to implement a novel method based on genetic programming to extract knowledge from experimental data based on the experience. This experience is implemented through constraints that are induced in the algorithm.
Acknowledgements.
This work was partially supported by the Spanish Ministry of Science and Innovation (Ref. BIA2010-21551) and grants from the Ministry of Economy and Industry (Consellería de Economía e Industria) of the Xunta de Galicia (Ref. 10MDS014CT, Ref. 10TMT042E, Ref. 10TMT118004PR and Ref. 10TMT034E).
References
1. Orangun, C.O., Jirsa, J.O., Breen, J.E.: A Reevaluation of Test Data on Development Length and Splices. ACI Journal 74(11), 114–122 (1977)
2. Tepfers, R.A.: Theory of bond applied to overlapped tensile reinforcement splices for deformed bars Ph.D. Thesis, Division of concrete structures, Chalmers University of Technology. Gothenburg, Sweden (1973)
3. Cairns, J.: Model for strength of lapped joints and anchorages. Paper presented at the meeting of the TG group 4.5 of the International Federation for Structural Concrete, Stuttgart, Germany (2006)
4. Abrams, D.A.: Tests of Bond Between Concrete and Steel. University of Illinois Bulletin Nº 71. University of Illinois, Urbana (1913)
5. FIB Task Group 4.5 “Bond models” (s.f) (2007), http://fibtg45.dii.unile.it/ (January 25, 2013)
6. Canbay, E., Frosch, R.: Bond strength of lap-spliced bars. ACI Structural Journal 102(4), 605–614 (2005)
7. Pérez, J.L., Cladera, A., Rabuñal, J.R., Martínez-Abella, F.: Optimization of existing equations using a new genetic programming algorithm: Application to the shear strength of reinforced concrete beams. Advances in Engineering Software 50(1), 82–96 (2012)
8. Ashour, A.F., Alvarez, L.F.: Toropov VV.: Empirical modeling of shear strength of RC deep beams by genetic programming. Computers & Structures 81(5), 331–338 (2003)
9. Pérez, J.L.: Metodología para orientar procesos de extracción de conocimiento basados en Computación Evolutiva. Aplicación al desarrollo de modelos y formulaciones en el ámbito del hormigón estructural, Ph.D. Thesis, Department of Information and Communication Technologies, University of A Coruña (2010).
10. Grandson, L.A. Taylor n-dimensional nets, The analytic equivalence to Neural Nets
10. Grandson, L.A. Taylor n-dimensional nets, The analytic equivalence to Neural Nets


No hay comentarios:
Publicar un comentario