Artículo patrocinado por Enmacosa dentro del proyecto "Formigón estructural", cofinanciado por la Xunta de Galicia (2013).
Article sponsored by Enmacosa inside the "Formigón estructural" project, cofinanced by the Xunta de Galicia. (2013)
Adherencia y Anclaje de acero de refuerzo en Hormigón Estructural / Bond and Anchorage of Reinforcing Steel in Structural Concrete
Autores / Authors: Juan Luis Pérez (1), Ismael Vieito (2), Juan Rabuñal (3), and Fernando Martínez-Abella (2)
1 School of Building Engineering and Technical Architecture, University of A Coruña, Spain
2 Department of Construction Technology, University of A Coruña, Spain
3 Department of Information and Communication Technologies, University of A Coruña, Spain
Abstract.
Partiendo de la base de datos FIB, este trabajo está dirigido a analizar las ecuaciones actuales que predicen el dato principal que puede ser proporcionada por los ensayos previos: El ensayo de rotura de probetas de hormigón. Además, la programación genética (GP) se aplica con el fin de mejorar la expresión de la FIB, que logra el mejor ajuste, hasta el momento, dando lugar al nuevo Código Modelo 2010. El resultado final que se muestra es una ecuación altamente predictiva. Los resultados se comparan con las incluidas en el Modelo y mostraron la influencia de las principales variables sobre el fenómeno (la resistencia del hormigón, límite elástico del acero, recubrimiento de hormigón, armadura transversal y el diámetro de la barra).
Starting from the FIB database, this work is aimed to analyze the current equations which predict the main datum that can be provided by bond tests: the ultimate bar stress when the failure is reached. Furthermore, Genetic Programming (GP) techniques are also applied in order to enhance the expression of the FIB, which achieves the best adjustment so far, giving rise to the new Model Code 2010. The final result shown is a highly predictive equation. The results are compared with those included in the Model Code and it is showed the influence of the main variables on the phenomenon (concrete strength, yield strength of steel, concrete cover, transverse reinforcement and diameter of the bar).
1 Introduction
Desde los albores del siglo 20, cuando se realizaron los ensayos de Abrams, el vínculo entre el hormigón y el acero dio lugar a numerosas publicaciones científicas, pruebas complejas de laboratorio y muchos enfoques de códigos estructurales. Hay muy pocas expresiones que son tan diferentes al comparar las diversas normas, como las destinadas a la predicción de la longitud de anclaje de las barras de refuerzo en el hormigón estructural. Dos líneas principales fueron creados a partir de los trabajos realizados por Orangun, Jirsa y Breen [1], precursores de la ecuación código ACI, y los estudios realizados por Tepfers [2], que inspiró a los lineamientos del modelo, que conduce a la Eurocódigo. Las pruebas llevadas a cabo en España también fueron de gran importancia, ya que dieron lugar a una formulación específica, extremadamente conservador para el refuerzo de gran diámetro.
Since the dawn of the 20th century, when Abrams’s tests were performed, the bond between concrete and steel led to numerous scientific papers, complex laboratory tests and many approaches of structural codes. There are very few expressions that are so different when comparing the various rules, such as those aimed at predicting the anchorage length of reinforcing bars in structural concrete. Two main lines were created starting from the works carried out by Orangun, Jirsa & Breen [1], precursors of the ACI code equation, and the studies performed by Tepfers [2], which inspired the guidelines of the Model Code, leading to the Eurocode. The tests carried out in Spain also were of great importance, as they gave rise to a specific formulation, extremely conservative for large-diameter reinforcement.
Since the dawn of the 20th century, when Abrams’s tests were performed, the bond between concrete and steel led to numerous scientific papers, complex laboratory tests and many approaches of structural codes. There are very few expressions that are so different when comparing the various rules, such as those aimed at predicting the anchorage length of reinforcing bars in structural concrete. Two main lines were created starting from the works carried out by Orangun, Jirsa & Breen [1], precursors of the ACI code equation, and the studies performed by Tepfers [2], which inspired the guidelines of the Model Code, leading to the Eurocode. The tests carried out in Spain also were of great importance, as they gave rise to a specific formulation, extremely conservative for large-diameter reinforcement.
A pesar de la variedad de enfoques, las tres líneas tienen un nexo común: las propuestas se desarrollan a partir de la evidencia experimental. A partir de una expresión fundamental de la tensión de adherencia, dependiente de una variable principal, se incorporan como un factor multiplicativo el efecto de otras variables. Cuando se realiza una prueba de extracción, un estado de tensión radial se genera alrededor de la barra que puede causar daño al hormigón circundante. El daño puede ser mitigado por la colocación de la armadura transversal. La figura 1 muestra gráficamente el fenómeno de una barra de anclaje [3]
Despite the varied approaches, the three lines have a common nexus: the proposals are developed from the experimental evidence. From a basic expression of bond stress, dependent on a main variable are incorporated as a multiplicative factor the effect of other variables When a pull-out test is performed, a state of radial tension is generated around the bar that can cause damage to the surrounding concrete. The damage can be mitigated by the placement of transverse reinforcement, and having adequate cover bar. Figure 1 shows graphically the phenomenon of a bar anchorage [3]
Despite the varied approaches, the three lines have a common nexus: the proposals are developed from the experimental evidence. From a basic expression of bond stress, dependent on a main variable are incorporated as a multiplicative factor the effect of other variables When a pull-out test is performed, a state of radial tension is generated around the bar that can cause damage to the surrounding concrete. The damage can be mitigated by the placement of transverse reinforcement, and having adequate cover bar. Figure 1 shows graphically the phenomenon of a bar anchorage [3]
 |
| Fig. 1. Fenómeno de un anclaje de barra. Fig. 1. Phenomenon of a bar anchorage |
2 Modelo FIB / FIB Model
El grupo de trabajo TG4.5 de la Fédération Internationale du Beton (FIB) [5] ha estado trabajando durante mucho tiempo en el análisis del anclaje y las características de la adherencia de las barras de acero de refuerzo. Basado en la obra de Canbay y Frosch [6], el grupo se ha propuesto dos ecuaciones: la versión de 2006 (1) y la versión actual empleada en la elaboración del Código Modelo 2010 (2), que proporciona la resistencia que puede ser alcanzado en una barra anclada. Esta ecuación depende de los parámetros observados hasta ahora y está protegido por un contraste con una base de datos experimental fuerte.Las variables descritas en ambas fórmulas corresponden a las tensiones de adherencia (σsu), resistencia a la compresión en probeta cilíndrica (Fc), diámetro de la barra (db), la longitud de la barra anclada (ls), máximo y recubrimientos mínimos de la barra (cmin, cmax) y el recubrimiento de la armadura transversal (KTR).
The workgroup TG4.5 of the Fédération Internationale du Beton (FIB) [5] has been working for a long time in the analysis of the anchorage and the bond characteristics of reinforcement steel bars. Based in the works of Canbay and Frosch [6], the group has proposed two equations: the version 2006 (1) and the current versi
on employed in the development of the Model Code 2010 (2), that provides the work stress that can be reached on an anchored bar. This equation depends on the parameters seen until now and is protected by a contrast with a strong experimental database.
The variables described in both formulas correspond to the bond stresses (σsu), compressive strength in cylindrical specimen (fc), diameter of the bar (db), length of anchored bar (ls), maximum and minimum coatings of the bar (cmin, cmax) and the contribution of the transverse reinforcement (Ktr).
2.1 Dataset
La base de datos contiene actualmente datos (variables y resultados medidos o calculados) correspondientes a 813 ensayos. Para aplicar técnicas GP para el análisis, el rango de la base de datos es consistente y las frecuencias de cada uno de los datos deben ser analizados. Teniendo en cuenta los datos de histograma de frecuencias, los filtros que se aplican y se aceptan son los recomendados por el FIB [5]. Uno de los más importantes está relacionada con la σsu, la tensión alcanzada por la barra durante la prueba. Cualquier probeta limita su máximo fy, la resistencia, el valor máximo que puede tener la relación σsu / fy es de 1.05. En otras variables de sus valores relativos también son limitados, por ejemplo, los relacionados con la cubierta de hormigón. Por lo tanto, se aplican los filtros sobre cmin / Cmax y Cmin / db. La Tabla 1 muestra los parámetros utilizados para el filtrado y el filtro finalmente aplicada.
The database currently contains data (variables and results measured or calculated) corresponding to 813 trials. As will be applied GP techniques for analysis, so that the database range is consistent and frequencies of each of the data must be analyzed. Considering the frequency histogram data, several filters are applied and are accepted those recommended by the FIB [5]. One of the most important is related to the output data σsu, the stress reached by the bar during the test. Since any bar limits its maximum stress fy, the maximum value that can take the relationship σsu/fy is 1.05. In other variables their relative values are also limited, for example those related to the concrete cover. Thus, filters over cmin/cmax and cmin/db are applied. Table 1 shows the parameters used for filtering and the filter finally applied.
 |
| Table 1. Filters applied to the dataset |
En las expresiones FIB BD filtrados producir resultados cuya precisión se presenta en las siguientes secciones.
After applying the filter, the BD is reduced to a total of 628 trials, of which 77.5% (487 trials), by random selection, are used for training, dedicating the remaining 22.5% (141 trials) to check. Table 2 shows the final range of the data in each of the subsets set (training and verification).
On the BD filtered FIB expressions produce results whose accuracy is presented in the following sections.
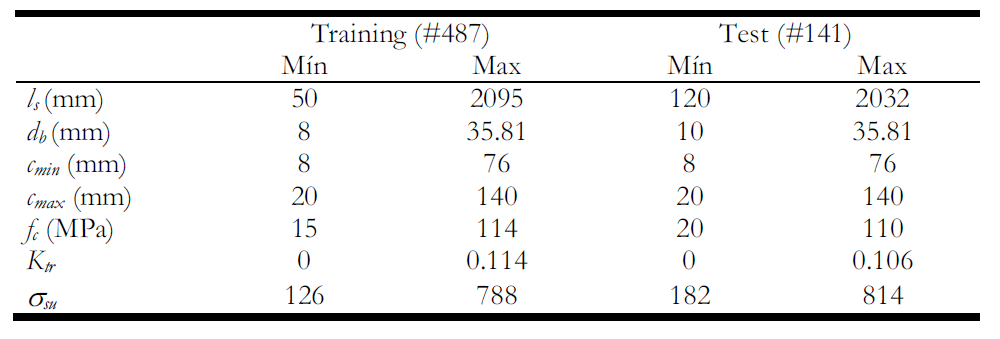 |
| Table 2. Distribution of data in subsets defined over the BD filtered |
3 Method
Continua en / Continue on: http://carreteras-laser-escaner.blogspot.com/2014/11/genetic-programming-to-improvement-fib_26.html
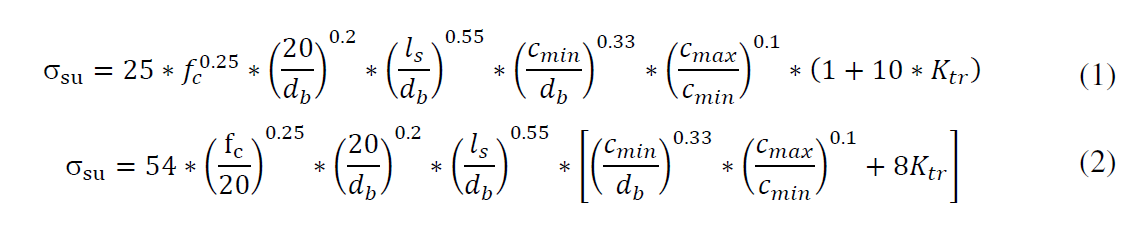
No hay comentarios:
Publicar un comentario