How to measure distances and absolute positions / Medir distancias y posiciones absolutas

Punto de partida

Starting point

Como ya viéramos tenemos:

What we have so far?

Proyecciones en diédrica

Pero en realidad queremos medir como si fuera el propio espacio tridimensional:

In fact we want to measure like 3D space itself:

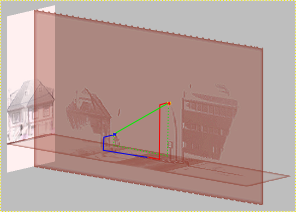Posiciones de puntos relativas y distancias entre ellos

Pasos a dar para conseguir este objetivo:
Steps to take to achieve this goal:

1º.- Saber calcular la posición absoluta desde una posición relativa (x e y):
1.- Know how to calculate the absolute position from a relative position (x and y):

Datos que se deben conocer:

• Punto O (Ox,Oy), Coordenadas absolutas del punto O.
• O bien el punto R, Coordenadas absolutas del punto R.
• Punto P, con coordenadas relativas al punto  R (origen de las coordenadas relativas

El problema consiste en pasar de P(Px,Py) a P'(P'x,P'y). el mismo punto en coordenadas absolutas. Se trata pues de un escalado, seguido de una rotación y una traslación:

En cálculo matricial P' = k · P · MR + MT, donde MR es la matriz de rotación y MT la matriz de tralación.

Data to be aware of:

• Point O (Ox,Oy), Absolute coordinates of the point O.
• Or point R, Absolute coordinates of the point R.
• Point P, with relative coordinates to the point  R

The problem is to move from P(Px,Py) a P'(P'x,P'y). the same point in absolute coordinates. It is therefore scaling, followed by a rotation and a translation:

In matrix algebra P' = k · P · MR + MT, MR: rotation matrix and MT: translation matrix.

      |P'x|    |Px||sen(a)  cos(a)| |Traslación x|
      |   |= k |  ||              |+|            |
      |P'y|    |Py||cos(a) -sen(a)| |Traslación y|

2º.- Para el caso de z, simplemente se suma la cota absoluta a la cota relativa (y claro está, se realiza después del escalado previo.
2º.- For z, simply adds the absolute coordinate relative dimension (and of course, after scaling is performed previous).

3º.- Sólo falta conocer la posición relativa, es decir hay que conocer la posición en píxeles del punto P al O según los ejes (girados) definidos en R.
El programa que hagamos debería, pues, darnos estas posiciones relativas y hacer después los cálculos.
Nuestro programa incorpora las imágenes de la forma:


3º.- Just need to know the relative position. You have to know the position in pixels from point P to O along the axes (rotated) defined in R.
The program should give us to do these relative positions and do after the calculations.
Our program incorporates the images of the form:

      <img ...> y debemos cambiarla a/change to <img id="a" onclick="subrutina_de_posicion()"...>

      ( o también / or <img id="a" onmousedown="subrutina_de_posicion()"...>

y dentro de la sección de scripts:
and within the scripts section:

<script>
...
function subrutina_de_posicion(){
function Position_subroutine(){
      var offset = $("#a").offset();
      Px=offset.left;
      Py=offset.top;

... poner aquí los cálculos que debe hacer
...put here the calculations.
}
...
</script>

NOTA: He utilizado a jQuery. Se incluye de la forma:

NOTE: I used to jQuery. Form includes:

<script language="javascript" src="...jquery.js">

4º.- Ejemplo real: pincha aquí
4º.- Real example: click here

Después de seleccionar puntos en las proyecciones se obtienen sus coordenadas

La idea es ir pinchando en cualquier proyección para obtener sus coordenadas relativas. Después el código de javascript hará los cálculos de homotecia, giro y traslación para conocer las coordenadas absolutas. En la figura se hace en dos puntos y además tendremos distancias (tanto en planta como en 3D). Claro está que para este último cálculo no hace falta ni el giro ni la traslación ya que en coordenadas relativas también se pueden evaluar distancias.

A partir del día 31 de enero de 2013 se añade otra utilidad previa al dimensionamiento por perfiles típico. Para ello se ha modificado la función "laplace" para ajustar el borde:

Inicialmente teníamos:

The idea is to go clicking on any projection to obtain their relative coordinates. After javascript code calculations will dilation, rotation and translation for absolute coordinates. The figure makes two points and you'll have distances (both in plan and 3D). It is clear that for this last calculation goes without rotation or translation as relative coordinates can also be evaluated distances.

Starting on January 31, 2013 will add another useful pre-dimensioning of typical profiles. This function has been modified "laplace" to set the border:

Initially we had:

Ahora, además tenemos:
Now, we also have:

Se observa que, en la proyección frontal, si dejáramos la línea inferior y hubiéramos tomado proyecciones cada menos intervalo (1 metro, en vez de 10) tendríamos definido el perfil transversal.
(cuando haya tiempo programaremos la salida a dxf o dwg)

It notes that in the frontal projection, if we let the bottom line and would have taken less projections each interval (1 meter instead of 10) would have defined the transverse profile.
(when you schedule the departure time to dxf or dwg)