Vamos a plantearnos un reto. Supongamos que disponemos de un conjunto de tres elementos ordenados en fila, por ejemplo {1, 2, 3} y ponemos una regla simple: A cada paso sólo pueden intercambiar el orden dos elementos contiguos. La pregunta que podríamos hacernos sería ¿Cuáles serían los pasos mínimos necesarios para disponer de todas las posibilidades de orden.
En el ejemplo dado habría que buscar la forma de obtener las 6 posibles formas de ordenar estos 3 elementos. Es decir, 123, 132, 213, 231, 312 y 321. Pero recordando la regla, sólo un intercambio de dos elementos contiguos cada vez.
Un solución sería: 123, 132, 312, 321, 231, 213. Si la visualizáramos en un grafo esta solución se vería más fácil:
Llegado a este punto resulta fácil percatarse de que dicha solución es única si nos permitimos decir que la simétrica es la misma solución o si se empezara desplazado un paso.
CUATRO ELEMENTOS.
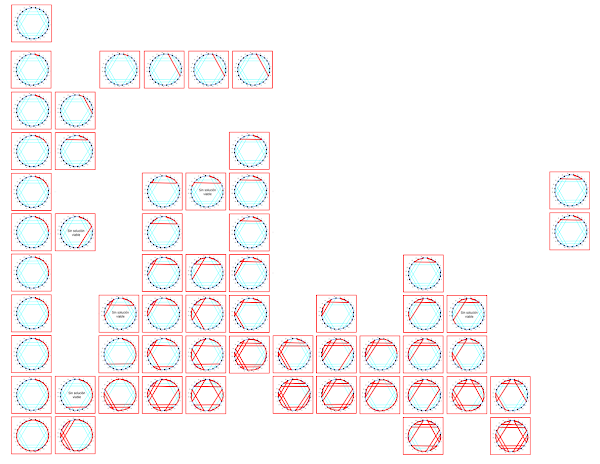
La cosa se complica cuando disponemos de cuatro elementos {1, 2, 3, 4} (NOTA: A veces pongo {0, 1, 2 3} Total, el uso de números es sólo gráfico no significan nada). Después de muchos intentos llegamos a la conclusión de que sólo hay cuatro maneras de disponer de los 24 conjuntos ordenado posibles de 4 elementos. Estos son:
En próximas entregas se demostrará que sólo pueden existir estas cuatro maneras de conseguir los 24 elementos diferentes de las 24 (4!) formas diferentes de disponer 4 elementos distintos. Para ello se utilizará sistemas de grafos.
Se supone que una solución simétrica, antisimétrica o desplazada de las anteriores es la misma solución.
Nota: Aún es pronto para atreverse a 5 elementos (5!=120 ordenaciones diferentes)