El paso siguiente es tomar uno de los sistemas de ordenación y basar el resto de sistemas en éste. Se toma el sistema "α":
Se ha supuesto un orden de las 24 formas en que se pueden ordenar los elementos del conjunto {1, 2, 3, 4}.Éstos van recorriendo la línea azul oscuro. Las líneas azul claro serían "atajos", otras posibilidades.
Lo mejor es verlo tomando un punto, por ejemplo el 9: [1423] si se cambian dos contiguos de la serie α serían el 8: [1243] o el 10:[4123] y no contiguo de la serie sería el 16:[1432].
El plan para buscar otras soluciones sería bastante simple. Hay que imaginar que los puntos son clavos y que lo que se quiere es recorrer todos los puntos con un hilo sin pasa dos veces por el mismo punto y por los caminos azules (claros u oscuros).
Aclaración: se ha establecido este sistema ya que sería más simple que aplicar la fuerza bruta. 24 cruces en tres posiciones cada uno sería 324 = 282.429.536.481. Y si se tuviera en cuenta que una de la posiciones no pudiera repetirse sería 224 = 16.777.216.
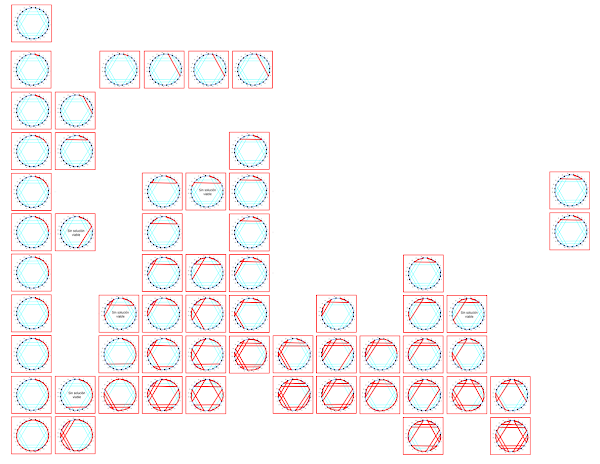
La forma de ir buscando soluciones sería ir tomando camino y descartando el resto, de la forma:
Ésta es sólo una parte. Al ir buscando recorridos cerrados se van encontrando soluciones y al descartar las repetidas se obtiene un pequeño número de recorridos:
Se subraya la palabra cíclica porque si no se deseara que el final de los cambios volviera al principio habría alguna solución más como la siguiente:
¿Y si no fuera una solución cíclica?
Un sólo contraejemplo daría pie a buscar las posibles soluciones no cíclicas. En la figura superior hay una. La cuestión ahora es saber cuantas más habrá. Pero eso quedará explicado en otro momento.
No hay comentarios:
Publicar un comentario