Cálculo de la función inversa partiendo de transmutaciones de matrioskas

Dada una función f(x) nos proponemos encontrar la función inversa f^-1(x) utilizando la transmutación de matrioskas de f(x)

La sucesión de matrioskas sería:

M₀(x)=x; M₁(x)=f(x); M₂(x)=f(f(x)); M₃(x)=f(f(f(x))); ….

Partiendo de la idea de transmutación de funciones:

Me(x)=P₀(e)·M₀(x)+ P₁(e)·M₁(x)+ P₂(e)·M₂(x)+…+ P_n(e)·M_n(x)

Dado que M_-1(x) = f^-1(x) → 

→ f^-1(x) = M_-1(x) = M_-1 (x)=P₀(-1)·M₀(x)+ P₁(-1)·M₁(x)+ P₂(-1)·M₂(x)+…+ P_n(-1)·M_n(x)

Esta aproximación será más exacta cuanto mayor sea al numero n;

Ejemplo  f(x)=seno(x)

Lo mejor será ver un ejemplo

Sea f(x)=seno(x)

Con dos matrioskas M₀; M₁

Con tres matrioskas M₀; M₁; M₂

Con tres matrioskas M₀; M₁; M₂; M₃

Con cuatro matrioskas M₀; M₁; M₂; M₃; M₄

¿Cuanto mayor sea el conjunto de matroskas, menor será el error?

¿Podemos cuantificar inicialmente el error?

¿Es necesario calcular los polinomio P0(e) ...Pn(e) o bastaría con saber los valores P0(-1) ...Pn(-1)?

¿Para cada una de las aproximaciones habrá un valor que e=-1 con el que se obtenga un menor error?. Si es así ¿Por qué?

¿Todos estos cálculos son realmente indiferentes a f(x)?

¿Cómo se adapta a la completitud de la función en el campo complejo?

Estas cuestiones las iremos resolviendo en las próximas entregas, 

Transmutación de funciones. Polinomios de escala

Como íbamos viendo del punto anterior:

T_e=E₁(e)f₁(x)+ E₂(e)f₂(x)+ E₃(e)f₃(x)+ E₄(e)f₄(x)+… = Σ E_i(e)f_i(x)

Es define E_i,g(e) Polinomio de escala de grado “g” para f_i(x).

Lo único que tienen que cumplir es que E_i,g(e)=1 si e=g; y E_i,g(e)=0 si e≠g;

Para ello vamos a empezar desde lo más fácil:

E_1,0(e) = 1

E_1,1(e) = -(e-2) = -e +2

E_1,2(e) = 1/2(e-2)(e-3)= 1/2e²-5/2e+3

E_1,3(e) = (-1/6)(e-2)(e-3)(e-4)

E_1,4(e) = (1/24)(e-2)(e-3)(e-4)(e-5)

E_1,g(e) = ((-1)^g/g!)(e-2)(e-3) … (e-g)

E_2,0(e) = No existe

E_2,1(e) = (e-1)

E_2,2(e) = -(e-1)(e-3)

E_2,3(e) = (+1/2)(e-1)(e-3)(e-4)

E_2,4(e) = (-1/6)(e-1)(e-3)(e-4)(e-5)

E_2,g(e) = ((-1)^(g-1)/(g-1)!)(e-1) (e-3) (e-4) … (e-g)

E_i,g(e) = K_i,g · (e-1)(e-2) … (e-(i-1))(e-(i+1)) … (e-g) 
y ... se calcula K_i,g para que E_i,g(e)=1 si e=g; (para el resto de valores es obviamente 0)

NOTA IMPORTANTE: en este punto hay que darse cuenta de que no necesitamos conocer ninguna f_i(x).

Tabla de coeficiente K hasta grado 10:

Pronto calcularemos inversas partiendo de Matrioskas...

Frecuencias fundamentales. Manual de Instrucciones.

Con la intención de no eclipsar el resto de apps de Abakal en Google Play Store esta app se distribuirá bajo demanda. Si la desea, diríjase a nosotros utilizando la sección de contacto:

https://carreteras-laser-escaner.blogspot.com/p/contacte-con-nosotros.html

Google play:

https://play.google.com/store/apps/details?id=nieto.luis.fundamental&hl=es_419

Historia / History

Hace tiempo, un amigo me mandó el siguiente enlace:
Some time ago a friend sent me the link below:

http://estructurando.net/2014/06/23/como-obtener-las-frecuencias-fundamentales-de-una-estructura-con-tu-smartphone/

Me pareció sumamente interesante y, al mismo tiempo, mágico. Recomendamos, por lo tanto su lectura.
I found it extremely interesting and, at the same time, magical. Recommended, therefore its reading.

También me dio rabia que no pudieran hacerse todos los cálculos con el propio teléfono. Por ese motivo nos atrevimos a crear nuestra propia aplicación.
I was also angry that all the calculations could not be done with the phone itself. For that reason we dared to create our own application.

Objetivos / Goals

Nuestro objetivo era registrar las vibraciones con un muestreo de 200 lecturas por segundo. y de esta onda obtener las frecuencias fundamentales.
Our goal was to record the vibrations with a sampling of 200 readings per second. And from this wave to obtain the fundamental frequencies.

Limitaciones / Limitations

El primer fracaso lo tuvimos al querer sobrepasar los 50 Hz de  muestreo. Nuestros dispositivos se bloqueaban. Probamos con otros programas para ver si éramos nosotros los que éramos incapaces de programar por encima de 50 Hz. Resultó inviable. El problema no estaba en la programación sino en el propio dispositivos. Algunos dispositivos alcanzaban los 100Hz de muestreo pero al cabo de un rato registrando terminaban bloqueándose.
The first failure was when we wanted to exceed 50 Hz of sampling. Some of our devices were blocked. We tested with other programs to see if we were the ones who were unable to program above 50 Hz. It turned out to be unfeasible. The problem was not in programming but in the device itself. Some devices reached 100Hz sampling but after a while recording ended up blocking.

Por los motivos anteriormente expuestos hemos limitado el muestreo a 50Hz. No podemos publicar una aplicación que bloquee dispositivos ajenos.
For the above reasons we have limited sampling to 50Hz. We can not publish an application that blocks third-party devices.

Instrucciones / Instructions 

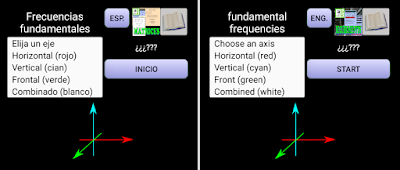
La pantalla inicial es la siguiente (dependiendo de la elección del idima: inglés o español)
The initial screen is the following (depending on the choice of the idima: English or Spanish)

Posibles elecciones: / Possible choices

Ejes Axis

• Horizontal (rojo/red)
• Vertical (cian/cyan)
• Frontal (verde/green)
• Conjunto/Combined (blanco/white)

Si conocemos la dirección predominate de la vibración mide mejor en su eje, (ya sea en la dirección horizontal, vertical o frontal) que en la conjunta.
If we know the predominant direction of vibration, it measures better on its axis (either in the horizontal, vertical or frontal direction) than in the combined.

Muestreo / Sampling

• 10 Hz
• 20 Hz
• 50 Hz

Procedimiento / Procedure

1º.- Elegimos el eje
2º.- Elegimos la frecuencia de muestreo.
3º.- Pinchamos sobre el botón "Inicio".
      - Empezarán las lecturas y el botón cambiará a denominarse "Toma de datos"
4º.- Pinchamos sobre "Toma de datos"
      - Comienza el registro de datos y el botón cambia a denominarse "Espere"
5º.- Mientras se denomine "Espere" no puede interactuar con el programa
6º.- Cuando tiene datos suficiente el botón cambia a denominarse "Parada"
7º.- El programa sigue registrando. Cuando lo consideremos suficiente pulsaremos sobre "Parada"
      - El programa nos preguntará si queremos los datos con punto (.) o coma (,) decimal
      - Elegimos una de las opciones
      - Nos comunicará donde fueron guardados los datos
         (valores de la onda y analizador de frecuencias en formato csv y png)
8º. El boton "Parada" cambiará a "Inicio". Fin del ciclo

1st. We chose the axis
2nd. We choose the frequency of sampling.
3th. Click on the "Start" button.
       - The readings will begin and the button will change to be called "Data acquisition"
4th. We click on "Data acquisition"
       - Data logging starts and the button changes to be called "Wait"
5th. While it is called "Wait" you can not interact with the program
6th. When you have enough data, the button changes to "Stop"
7th. The program continues to register. When we consider it sufficient we will press on "Stop"
       - The program will ask us if we want the data with point (.) or comma (,) decimal
       - Choose one option
       - Tell us where the data was stored
          (Wave values and frequency analyzer in csv and png format)
8th. The "Stop" button will change to "Start". End of cycle

Resultados / Results

El programa guardará los siguientes archivos:
The program will save the following files:

Cuya nomenclatura variará según la selección de idioma (español o inglés) 

Whose nomenclature will vary depending on the language selection (Spanish or English)

Podemos abrir nuestro informe denominado Frecuencimetro.cvs con nuestra hoja de cálculo preferida y volver a crear la gráfica:

We can open our report called Frecuencymeter.cvs with our favorite spreadsheet and re-create the graph:

Podemos, simplemente, ver nuestra gráfica Fundamentales.png;
We can simply see our graph Fundamental.png;

Podemos abrir nuestro informe denominado Onda.cvs con nuestra hoja de cálculo preferida y crear la gráfica de la onda:

We can open our report called Wave.cvs with our preferred spreadsheet and create the graph of the wave:

AVISO IMPORTANTE / IMPORTANT WARNING

La capacidad de refresco del acelerómtero interno no depende del precio de nuestro dispositivo.
Si note que se bloquea, desinstálelo. Puede que le estemos pidiendo demasiado a su dispositivo.
En ningún caso usted tiene un vibrómetro profesional, por lo que la medición que obtenga será siempre aproximada.
The ability to refresh the internal acelerómtero not depend on the price of our device.
If note that crashes, uninstall it. You may find we're asking too much of your device.
In no case you have a professional vibrometer, so the measurement you get will always be approximate.

Transmutación de funciones

Con este título tan rimbombante hemos querido empezar a gestionar un problema matemático que nos parece muy interesante. Se trata de buscar la secuencia de funciones que permiten de forma continua transformar una función en otra.

Planteamiento:

Dada una función origen f(x) y otra función destino g(x) definiremos T₁=f(x) y T₂=g(x). La forma más sencilla de transmutación seria de tipo lineal:

T_e=-(e-2)f(x)+(e-1)g(x)

Que en el caso de f(x)=sen(x) y g(x)=x²/2-2 nos darían unas gráficas del siguiente estilo:

Si volviéramos al artículo anterior con el tema de las funciones Matrioskas. Con el caso particular de M_n= a^αx^β con f(x)=ax^b, donde α=b^n-1+b^n-2+…+b+1=(bⁿ-1)/(b-1),, β=bⁿ. Podríamos comprobar su grado de aproximación.

Sea f(x)=3x² ,

Me=3^(2^e-1)*x^(2^e)

T_e=-(e-2)3x² +(e-1)27x⁴ 

Sorprende ver la similitud entre ambas transformaciones:

Claro está que podemos añadir una función más a la transmutación de funciones. 

Incorporemos una tercera.

1º Sea el trío de funciones f(x)=seno(x), g(x)=x²/2-2 y h(x)=cos(2x).

2º Definiremos T₁=f(x), T₂=g(x) y T₃=h(x).

3º Buscaremos la más simple transmutación con polinomios e de segundo grado:

4º Solución: T_e=0.5(e-2)(e-3)f(x) -(e-1)(e-3)g(x) + 0.5(e-1)(e-2)h(x)

Por otro lado, si volvemos a nuestro ejemplo de Matrioska con un trío de funciones:

Me=3^(2^e-1)*x^(2^e)

T_e=0.5(e-2)(e-3)3x² -(e-1)(e-3)27x⁴ -(e-1)(e-2)243x⁸ 

Observaremos que aproxima mejor:

En las siguientes entregas veremos que en nuestra fórmula general:

T_e=E₁(e)f₁(x)+ E₂(e)f₂(x)+ E₃(e)f₃(x)+ E₄(e)f₄(x)+… = Σ E_i(e)f_i(x)

1.- Cómo se calculan fácilmente los polinomios de escala  E_i(e) 

2.- Cómo se calcula una inversa cualquiera con transmutación y Matrioskas

3.- Otra forma de buscar subderivadas

Funciones Matrioskas

Como ya viéramos con la  derivación fracionaria (Véase: http://carreteras-laser-escaner.blogspot.com.es/2014/10/fractional-continuous-derivatives.html) ahora vamos a intentar hacer lo mismo con las funciones Matrioskas

Definición ¿Qué es?

Una función Matrioska está definida como la función de funciones cuyo índice indica el grado de anidamiento de una función en sí misma. La denominación más extendida es función recurrente y en programación se denomina recursividad. Aquí lo que queremos es añadir el concepto de grado de recursividad en una nueva función denominada Matrioska en la que se incorporará como parámetro de la misma.

Veámos un ejemplo:

Sea f(x)=x²+1

M₁(f(x))= x²+1

M₂(f(x))= (x²+1)²+1=x⁴+2x²+2

M₆(f(x))=f(f(f(f(f(f(x))))))

Propiedades por coherencia

Como 

M_a(M_b(f(x))=M_a+b(f(x))

Por coherencia .si M₀(M_b(f(x))=M_0+b(f(x))=M_b(f(x))

M₀(f(x))=x, ∀ f(x). Sería nuestra Matrioska neutra.

Si M_a(M_-1(f(x))=M_a-1(f(x)), eliminar un anidamiento equivale a aplicar una inversa

M_-1(f(x))=f^-1(x), es decir la inversa.

La continuidad del índice ¿ i € ℜ ó sólo i € Z?

Al igual de lo que sucediera con las subderivadas, nuestra intención es la de buscar la continuidad del subíndice.

Esta tarea resulta francamente difícil, imposible a priori. Aún no hemos encontrado un método eficaz de calcularla. (en las futuras entregas veremos que sí) hay métodos aproximados).

Para casos sencillos como por ejemplo con f(x)=ax^b.

M₂= a(ax^b )^b =a^b+1x^b2

M_n= a^αx^β,, donde α=b^n-1+b^n-2+…+b+1=(bⁿ-1)/(b-1),, β=bⁿ.

Caso particular: M_0.3(3x⁵)=1.1859x^1.62065.   Ya que α=(5^0.3-1)/(5-1)=0.552 → 3^0.552=1.1859. 

En el momento en que se complica un poco Por ejemplo, con f(x)=x²+1. No sólo se vuelve cansino transcribir M10(x²+1) sino que resultará aparentemente imposible conseguir M0.3(x²+1)