(Operador ֎)
Por lo vistoso se va a mostrar el efecto en vectores 3D.
Al multiplicar el vector (a,b,c) ֎ (1,0,0) queda (a,b,c), trivial ya que es el elemento neutro.
Al multiplicar el vector (a,b,c) ֎ (0,1,0) queda (c,a,b,), cambio de ejes.
Al multiplicar el vector (a,b,c) ֎ (0,0,) queda (b,c,a), el otro cabio de ejes.
El siguiente paso es como variar progresivamente de (1,0,0) a (0,1,0). Se va a imponer una condición más y es que el módulo del vector resultante sea el mismo que el original:
(a,b,c) ֎ (u,v,0)=(au+cv, bu+av, cu+bv)
Igualando los módulos, antes y después (y conservando el cuadrado para no meterse en raíces):
a2+b2+c2 = (au+cv)2 + (bu+av)2 + (cu+bv)2
Las condiciones que se deben cumplir son:
u2 + v2 = 1
c = -ab / (a+b)
La primera condición (u2+v2 = 1) se cumple con las funciones seno y coseno.
Para visualizarlo se muestra el siguiente ejemplo:
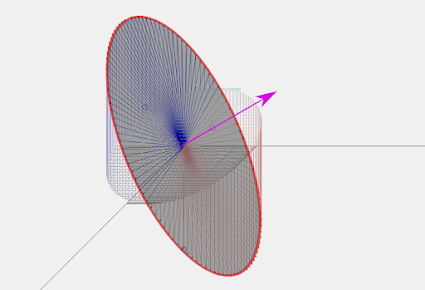
No hay comentarios:
Publicar un comentario