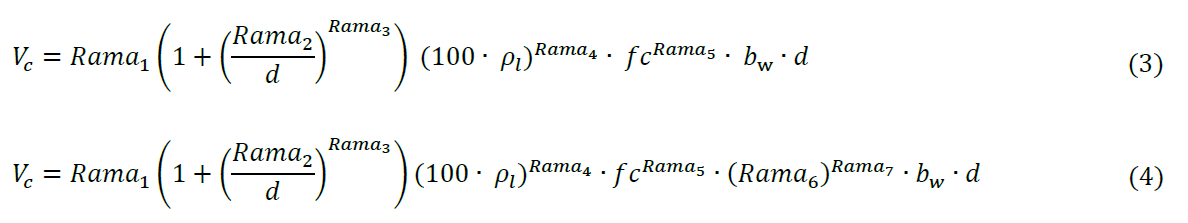Artículo patrocinado por Enmacosa dentro del proyecto "Formigón estructural", cofinanciado por la Xunta de Galicia (2013).
Autores: Juan Luis PÉREZ ORDÓÑEZ, Antoni CLADERA BOHIGAS, Juan R. RABUÑAL DOPICO, Fernando MARTÍNEZ ABELLAResumen
En este artículo se presenta el método empleado en la mejora de la formulación del Eurocódigo 2 que determina la resistencia a cortante en vigas de hormigón estructural sin armadura transversal. Se emplean para ello técnicas de Programación Genética (PG), mejoradas con módulos que dirigen el proceso de búsqueda. Se analiza qué términos de la expresión podrían ser mejorados y, mediante un conjunto de restricciones fijadas gracias a un conocimiento profundo del fenómeno, se inicia la creación de nuevas ecuaciones de modo orientado. Para el desarrollo y verificación de los modelos se han empleado cerca de 1200 ensayos de resistencia sobre vigas de hormigón. Se obtienen así sencillas expresiones, muy similares en forma a la conocida del EC-2 o la EHE-08, que incluyen la interrelación momento-cortante y mejoran el sentido físico de la expresión. Los resultados obtenidos se comparan con las predicciones del Eurocódigo 2 y el código ACI318-05.
1 Introducción
La resistencia a cortante de vigas de hormigón armado en elementos sin armadura transversal es, sin duda, uno de los aspectos más controvertidos ligado a los Estados Límite Últimos. Existe un amplio abanico de modelos teóricos de elevada complejidad que, debido a la dificultad de plasmar la importancia de todas las variables implicadas, derivan en diferentes propuestas normativas que en muchos casos son formulaciones de origen empírico, como es el caso de Eurocodigo 2 (EC-2) [1] y el código Americano (ACI 318-05) [2]. Algunas de las limitaciones del planteamiento del EC-2 son el que no se considere ni la interacción entre momentos flectores últimos y cortantes últimos ni el efecto del tamaño máximo del árido.
Una vez que una viga esbelta sin armadura transversal ha fisurado a cortante, existen diversos mecanismos de transferencia: las tensiones de corte en el hormigón no fisurado de la cabeza de compresión, el cortante transferido en la superficie de la fisura (conocido como engranaje de áridos o cortante-fricción), las tensiones de tracción residuales transmitidas directamente a través de las fisuras y el efecto dovela de la armadura longitudinal [3,4]
Por su sencillez y la correcta correlación frente a resultados experimentales en general, la ecuación dada en el EC-2 se está extendiendo a diferentes normativas nacionales y europeas, como es el caso de la Instrucción Española [5]. Una de las limitaciones que plantea, sin embargo, es el hecho de no considerar interacción entre momentos flectores últimos y cortantes últimos excepto para valores elevados del momento flector, en los que el cortante resistido disminuye al plastificar la armadura traccionada. Para una sección dada, según la formulación del EC-2, el cortante último es independiente del momento flector concomitante para momentos flectores alejados del que produce la plastificación de la armadura longitudinal. Por el contrario, modelos más complejos como la Modified Compression Field Theory (MCFT) [6] predicen, para una sección dada, una reducción del cortante de rotura a medida que aumenta el momento flector concomitante para cualquier valor del momento flector (ver Figura 1).
 |
| Figura 1. Interacción momento cortante según formulación EC-2 y MCFT. |
El tratamiento de la influencia de la cuantía de armadura longitudinal varía también notablemente de una normativa a otra. La formulación dada por el EC-2 propone que la resistencia a cortante es proporcional a la cuantía de armadura longitudinal. Sin embargo, otros modelos reflejan que el cortante último es proporcional al valor ρlVd/M, como se hace en uno de los métodos propuestos en el Código ACI. En el dimensionamiento real de vigas, la cuantía de armadura longitudinal crece proporcionalmente con el momento flector concomitante y, por tanto, el parámetro ρlVd/M es prácticamente constante. Sin embargo, es habitual en ensayos de laboratorio utilizar valores de ρl desproporcionadamente elevados para evitar roturas a flexión e, incluso, realizar series de ensayos en los que a/d disminuye, mermando por tanto el momento flector concomitante, sin variar el armado longitudinal. Por este motivo, algunos autores [7] sostienen que el ajuste de ecuaciones con estos ensayos no realistas puede producir desviaciones para elementos reales con las combinaciones habituales de las distintas variables. En el caso de la formulación dada por el EC-2, un aumento de la cuantía longitudinal supondría siempre un incremento en la resistencia a cortante independientemente del momento flector concomitante.
2 Programación Genética
La Programación Genética (PG) es un subconjunto de técnicas de búsqueda de soluciones enmarcadas dentro del campo de Computación Evolutiva (CE) que permite realizar, entre otras funciones, regresión simbólica a partir de patrones de aprendizaje. La CE engloba un conjunto de métodos basados en modelos que emulan ciertas características de la naturaleza, fundamentalmente la capacidad que poseen los seres vivos para adaptarse a su ambiente. Esta característica de los seres vivos ya había sido plasmada por Charles Darwin en su teoría de la evolución según el principio de selección natural de las especies [8]. Darwin sostiene que aquellos individuos de una población que posean las características más ventajosas dejarán proporcionalmente más descendencia en la siguiente generación, y si tales características se deben a diferencias genéticas que pueden transmitirse a los descendientes, tenderá a cambiar la composición genética de la población, aumentando el número de individuos con dichas características. De esta forma, la población completa de seres vivos se adapta a las circunstancias variables de su entorno. El resultado final es que los seres vivos tienden a perfeccionarse en relación con las circunstancias que los envuelven.
En la PG se establece una analogía entre el conjunto de soluciones de un problema y el conjunto de individuos de una población natural, codificando la información de cada solución mediante una estructura denominada “árbol”. Por ejemplo la Figura 2 representa una posible solución a un problema donde se desea relacionar las variables de entrada (a, b) con la salida f(a,b) mediante la expresión f(a,b) = a*((b/4)+3)). En este ejemplo los nodos no terminales o funciones corresponderían al producto, la suma y la división, mientras que los nodos terminales (u hojas del árbol) se corresponden con los valores 3 y 4, junto con las variables a y b. Por lo tanto, una parte fundamental de la configuración de la PG para su ejecución es la especificación del conjunto de elementos terminales y no terminales antes del inicio del proceso evolutivo, puesto que el algoritmo construirá los árboles con los nodos que se le especifique.
 |
| Figura 2. Árbol para la expresión a*((b/4)+3)). |
Los autores han presentado un algoritmo [9,10] basado en técnicas clásicas de Programación Genética, pero especializado en la optimización de fórmulas matemáticas. Dicho algoritmo permite, a partir de datos experimentales, la mejora de una expresión matemática bajo la supervisión de un experto, conduciendo el proceso de búsqueda de nuevas soluciones mediante restricciones aportadas por tal experto. En síntesis, dada una expresión, se seleccionan uno o varios términos de la fórmula a mejorar, se establece un conjunto de restricciones que debe cumplir cada uno de esos términos, y, con ayuda del algoritmo mediante un proceso iterativo, se consigue mejorar la ecuación inicial. En la Figura 3 se muestra un esquema del método empleado.
 |
| Figura 3. Esquema del método empleado. |
3 Aplicación de la técnica
3.1 Eurocódigo 2Eurocódigo 2 Eurocódigo 2 Eurocódigo 2
En la ecuación (1) se muestra la formulación adoptada por el EC-2 en el caso de vigas sin esfuerzo axil, una vez eliminado el factor de seguridad, con la condición de que el valor obtenido como resultado de aplicar la ecuación (1) siempre sea mayor que el valor mínimo dado por la ecuación (2). En la Tabla 1 se muestran las distintas variables empleadas en esta formulación.
 |
| Tabla 1. Variables empleadas en el modelo del Eurocódigo 2 |
Para abordar la mejora del EC-2 se han establecido las ecuaciones (3) y (4). La ecuación (3) proviene directamente de la generalización de la formulación del EC-2 (1), donde Ramai indica la posibilidad de que aparezca una expresión formada por las variables consideradas, en las condiciones definidas en 3.3. En cambio, en la ecuación (4) se ha añadido un nuevo término, (Rama6)^Rama7, con el que se pretende introducir la influencia de la relación entre el esfuerzo cortante y el momento flector concomitante.
3.2 Conjunto de datos
Para la mejora de la ecuación del EC-2 se ha empleado principalmente una base de datos recopilada por Collins et al. [7]. Las variables utilizadas son las contempladas por el EC-2 (bw, d, fc y ρl), y la variable V·d/M, que tiene en cuenta la relación entre el cortante y el momento flector concomitante en la sección crítica y que es fácilmente deducible a partir de la luz a cortante del ensayo y el tipo carga. El resultado es el cortante experimental de rotura, Vu.
La mayoría de las vigas que constan en las bases de datos son vigas rectangulares simplemente apoyadas bajo cargas concentradas, si bien también hay ensayos con carga repartida o sección en T.
Una vez recopilados los ensayos se han eliminado aquellos en los que las roturas no se hayan identificado como rotura a cortante. De igual manera no se han considerado todos los ensayos cuya relación a/d, donde a es la luz a cortante y d el canto efectivo, es menor que 2,5. Tras estos dos filtros el conjunto total de datos está formado por 1149 vigas. Este conjunto, a su vez se subdivide en 2, el primero de 518 vigas empleado para el entrenamiento, y el segundo de 613 destinado a verificar los resultados obtenidos. Esta división se ha realizado de forma aleatoria, con la salvedad de que el conjunto de entrenamiento abarcase los rangos de variables de conjunto total. En la Tabla 2 se muestran las características de ambos conjuntos.
 |
| Tabla 2. Conjunto de datos empleado . |
3.3 Configuración de PG
Después de un conjunto de pruebas iniciales se ha establecido que la configuración con mejores resultados (por término medio) emplea un tamaño de población de 1000 individuos, una tasa de cruces del 80%, una tasa de selección de un nodo no terminal del 90%, y una probabilidad de mutación del 20%. Las mismas pruebas determinan los algoritmos con mejor comportamiento: la selección mediante torneo, la creación según un método intermedio y la mutación a través de un algoritmo basado en subárbol. Siempre se ha empleado una estrategia elitista, garantizando de esta manera que el mejor individuo de cada iteración se traslade a la siguiente. La altura máxima permitida de los individuos ha sido de nivel 6, pudiendo llegar al nivel 10 en alguna de las pruebas. En cambio, la altura máxima en la que se permite realizar la mutación se ha establecido en el nivel 3, llegando al nivel 8 en algunos casos. En función de las alturas y las restricciones que se mostrarán en este apartado, el valor de la parsimonia se estableció entre 0 y 0,1. Cabe resaltar que el conjunto de datos empleado no ha sido normalizado.
Por defecto se ha elegido como operadores o nodos no terminales la suma, resta, producto y división protegida [10]. Para los nodos terminales se emplean las variables procedentes del conjunto de datos (d, fc, ρl y V·d/M), cualquier constante real aleatoria dentro del intervalo [-1, 1] y cualquier entero en el intervalo [-10, 10].
3.3.1 Restricciones
En la Tabla 3 se muestran las restricciones más representativas que se han impuesto empleando como base la ecuación (3). La abreviatura “Cte” indica que se permite el empleo de cualquier constante generada mediante PG, a base de operaciones suma, resta, multiplicación y división protegida, a partir de las definidas en el párrafo anterior. Con los símbolos de las variables d, fc o l (en la ecuación (3) se excluye la variable V·d/M) se permite que la Ramai adopte una expresión formada por esas variables y las constantes admitidas relacionadas mediante los operadores suma, resta, multiplicación y división protegida. Por último, cuando aparece un valor o expresión definidosse debe entender que sólo se empleará ese valor en esa rama.
 |
| Tabla 3. Restricciones aplicadas en la ecuación (3) |
La experiencia adquirida tras realizar las pruebas empleando como base la ecuación (3) ha conducido a establecer únicamente dos conjuntos de restricciones para la ecuación (4), presentadas en la Tabla 4.
 |
| Tabla 4.. Restricciones aplicadas en la ecuación (4) |