Investigación de Enmacosa dentro del proyecto "Desarrollo y mejora de modelos teóricos del hormigón estructural a partir de su dosificación mediante técnicas de programación genética y redes de neuronas artificiales", cofinanciado por la Xunta de Galicia (2010-2013).
Enmacosa research within the project "Development and improvement of theoretical models of structural concrete from its dosage by genetic programming and artificial neural networks", cofinanced by the Xunta de Galicia (2010-2013).
Continúa de: http://carreteras-laser-escaner.blogspot.com/2014/12/3-development-and-improvement-of.html
1 Introducción.
2 Seguimiento - Finalización.
3 método aplicado.
3.1 Fase 1. Identificación de variables clave ..
3.2 Fase 2. Análisis de los resultados
3.3 Fase 3. Aplicación de técnicas de regresión .
4 Resultados alcanzados.
4.1 Base de datos
4.1.1 Resultados.
4.1.2 Caracterización de base de datos
4.2 Variables que afectan a las propiedades del hormigón.
4.2.1 Las variables con alta influencia.
4.2.2 Variables que influyen en los medios de comunicación.
4.2.3 Variables con baja influencia.
4.3 Aplicación de RR.NN.AA. la predicción de parámetros físicos medibles mediante ensayos
4.4 Análisis de la resistencia alcanzado por los diferentes hormigones, en relación con la especificada
4.4.1 Análisis por el fabricante
4.5 Análisis de consistencia obtenidos con respecto como se especifica
4.6 Análisis de la evolución de la resistencia del hormigón con la edad
4.6.1 CEM I 52,5 R
4.6.2 CEM II 42.5 R
4.6.3 I / 52,5 N / SR
4.6.4 III / A 42,5 N / SR
4.6.5 IV / A-V 42,5 N / SR.
4.7 Análisis de la relación y el contenido de agua / cemento con la resistencia del hormigón.
4.8 Predicción del módulo del hormigón - Convencional
5 Publicaciones.
5.1 Mejora de la formulación de la EC-2 para la resistencia al corte en vigas de hormigón Estructural sin armadura.
5.2 Regresión simbólico en Ingeniería Civil a través de técnicas de programación genética.
5.3 Programación Genética para Modelo de Mejora FIB: Bond y Anchorage de refuerzo Acero Estructural en Concrete
6 Bibliografía
2 Seguimiento - Finalización.
3 método aplicado.
3.1 Fase 1. Identificación de variables clave ..
3.2 Fase 2. Análisis de los resultados
3.3 Fase 3. Aplicación de técnicas de regresión .
4 Resultados alcanzados.
4.1 Base de datos
4.1.1 Resultados.
4.1.2 Caracterización de base de datos
4.2 Variables que afectan a las propiedades del hormigón.
4.2.1 Las variables con alta influencia.
4.2.2 Variables que influyen en los medios de comunicación.
4.2.3 Variables con baja influencia.
4.3 Aplicación de RR.NN.AA. la predicción de parámetros físicos medibles mediante ensayos
4.4 Análisis de la resistencia alcanzado por los diferentes hormigones, en relación con la especificada
4.4.1 Análisis por el fabricante
4.5 Análisis de consistencia obtenidos con respecto como se especifica
4.6 Análisis de la evolución de la resistencia del hormigón con la edad
4.6.1 CEM I 52,5 R
4.6.2 CEM II 42.5 R
4.6.3 I / 52,5 N / SR
4.6.4 III / A 42,5 N / SR
4.6.5 IV / A-V 42,5 N / SR.
4.7 Análisis de la relación y el contenido de agua / cemento con la resistencia del hormigón.
4.8 Predicción del módulo del hormigón - Convencional
5 Publicaciones.
5.1 Mejora de la formulación de la EC-2 para la resistencia al corte en vigas de hormigón Estructural sin armadura.
5.2 Regresión simbólico en Ingeniería Civil a través de técnicas de programación genética.
5.3 Programación Genética para Modelo de Mejora FIB: Bond y Anchorage de refuerzo Acero Estructural en Concrete
6 Bibliografía
4.7 ANÁLISIS DE LA RELACIÓN Y DEL CONTENIDO AGUA/CEMENTO CON LA RESISTENCIA DEL HORMIGÓN
Es bien conocido que la resistencia de la unión depende de muchos factores. La dependencia es fuerte, media o baja según el tipo de pacto. No obstante la base de datos no proporciona valores a todas las variables consideradas. En la literatura científica hay varias fórmulas delictivas que reducen mucho las variables. Son las siguientes:
- Fórmula de Feret:
Donde R es la resistencia, K es un factor que depende de la resistencia do cemento, c es el peso del cemento, e es el volume de agua y v es el volumen de huecos.
- Fórmula de Abrams
- Fórmula de Bolomey:
- Fórmula de Dutron
Aceptando que la base de datos no proporciona volumen de huecos se dispone teóricamente de muchos datos que incluyen el contenido de cemento (c) y la relación agua/cemento (a/c). Como ya se explicó, a partir de estas fórmulas se aplicaron técnicas de redes neuronales información genética para intentar adaptar una impresión como la capacidad predictiva. Fue posible a pesar de las múltiples pruebas, dado que los datos no pueden considerarse ciertos. Éste es, en definitiva, uno de los grandes problemas del control de los fenómenos es decir, le conseguía disponer de una dosificación verificable. La medida de la resistencia es un buen criterio, pero no es suficiente para asegurar una durabilidad, ya que depende fuertemente c y de a/c.
Como ejemplo, se presenta a continuación los análisis realizados para observar la dependencia de resistencias con las variables c y a/c. Se selecciona una edad ensayo de compresión (28 días), un tipo de cemento (CEM I 52.5 R) y una resistencia característica (30 MPa). Sobre estos parámetros estudia la distribución de resultados con las variables c (325, 375, 425 kg/m3) y a/c (entre 0.31 e 0.6). El número de ensayos por cada caso son 1.796, 763, 307 respectivamente. En las siguientes gráficas se muestra la distribución.
Para una cantidade de cemento de 325 kg/m3, la relación a/c = 0.49 presenta la máxima frecuencia entre los 41 y 43 MPa. Para c = 375 kg/m3, l mayor frecuencia se observa en el intervalo 30 – 32 MPa para una relación a/c = 0.46. Y para c = 425 kg/m3, la mayor frecuencia se observa en el intervalo 38 – 40 MPa para una relación a/c = 0.46.
Os resultados muestran una inconsistencia fuerte, ya que a medida que aumenta c y se reduce a/c las resistencias deberían aumentar, y los datos no proporcionan esa tendencia.
Como ejemplo, se presenta a continuación los análisis realizados para observar la dependencia de resistencias con las variables c y a/c. Se selecciona una edad ensayo de compresión (28 días), un tipo de cemento (CEM I 52.5 R) y una resistencia característica (30 MPa). Sobre estos parámetros estudia la distribución de resultados con las variables c (325, 375, 425 kg/m3) y a/c (entre 0.31 e 0.6). El número de ensayos por cada caso son 1.796, 763, 307 respectivamente. En las siguientes gráficas se muestra la distribución.
 |
| Figura 31. Distribución para c= 325 kg/m3 |
 |
| Figura 32. Distribución para c= 375 kg/m3 |
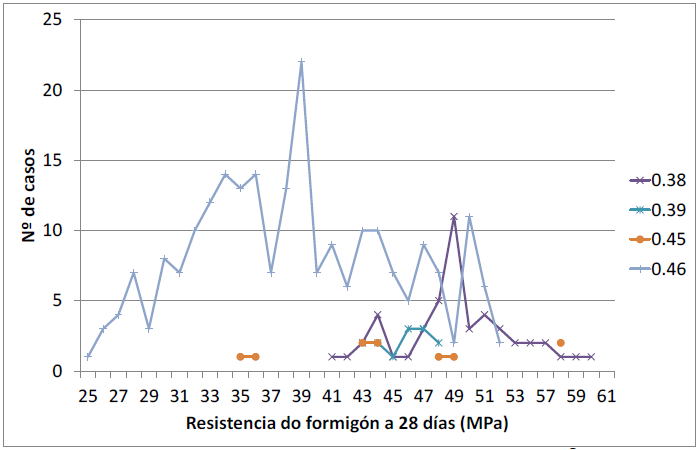 |
| Figura 33. Distribución para c= 425 kg/m3 |
Os resultados muestran una inconsistencia fuerte, ya que a medida que aumenta c y se reduce a/c las resistencias deberían aumentar, y los datos no proporcionan esa tendencia.
4.8 PREDICIÓN DEL MÓDULO DEL HORMIGÓN – CONVENCIONAL
A lo largo de la realización del proyecto se obtuvo un conjunto de datos experimentales realizados en el JCI (Japan Concrete Institute) En donde nos ensayaron diversas probetas en función de su dosificación obteniendo una resistencia a compresión y además el módulo de elasticidad (módulo de Young-E). El conjunto de datos es de 3071 ensayos, En los enormes 704 se dispone de un valor del módulo. Una vez hecho central depuración de los datos únicamente fueron áridos para el estudio 263 ensayos. En la tabla 18 se pueden ver los rangos empleados.
La normativa española actual (EHE) Para predecir el módulo a partir del valor de la resistencia a compresión emplea la ecuación (7), en cambio, otros autores (Kakizaki et al. 1988, Amnon Katz (2003) consideran que La densidad del hormigón matiza la predicción alcanzando mejores resultados (ecuaciones (8) y (9) respectivamente).
Teniendo en cuenta este hecho se planteó añadir esa nueva variable para mejorar la atención de hecho, a partir de la ecuación original de la EHE, en sentido como fenotipo la programación genética la ecuación (10), Donde se establecen 3 puntos (denominados ramas) En los que el algoritmo desarrollado podrá crear ecuaciones o constantes (en función das restricciones introducidas) para obtener unas mejores predicciones.
En este caso se establecieron las siguientes restricciones:
Tras ejecutar 200 veces el algoritmos de programación genética con la configuración que se muestra en la tabla 19 se llegó a que el mejor resultado es producido por la ecuación (11)
En la tabla 20 se muestran los resultados de las distintas métricas aplicadas a las ecuaciones existentes Mas la ecuación propuesta. Se puede observar que la propuesta tiene mayor capacidad predictiva. Finalmente la figura 24 se puede ver de forma gráfica la mayoría de las de bienes frente al actual EHE-08.
En este caso se establecieron las siguientes restricciones:
- Rama0: Constante entera
- Rama1: Constante real con dos decimales de precisión
- Rama2: Constante real positiva con dos decimales de precisión
Tras ejecutar 200 veces el algoritmos de programación genética con la configuración que se muestra en la tabla 19 se llegó a que el mejor resultado es producido por la ecuación (11)
En la tabla 20 se muestran los resultados de las distintas métricas aplicadas a las ecuaciones existentes Mas la ecuación propuesta. Se puede observar que la propuesta tiene mayor capacidad predictiva. Finalmente la figura 24 se puede ver de forma gráfica la mayoría de las de bienes frente al actual EHE-08.
 |
| Figura 34. Valor predicho contra valor real (EHE-08 y la ecuación propuesta) |
5 PUBLICACIONES
El proyecto desarrollado por ENMACOSA y por el grupo gCONS Cual soporte de una línea de trabajo fructífero en el campo de la inteligencia artificial aplicada al campo del hormigón estructural. Muchas de las técnicas desenvueltas se pudieron intensificar en un publicación el impacto, que de modo evidente Tiene su origen en este proyecto, aunque se empleen datos que no son estrictamente los que se analizaron en el desarrollo Metefores.
Consideramos por eso que entre las aplicaciones derivadas de este proyecto deben incluirse sin duda las que a continuación se relacionan que se nutren del conocimiento alcanzado. Las publicaciones con resultados propios de Metefores corresponden al análisis de datos de productos y fabricantes de organizaciones se tramitarán.
5.1 MELLORA DE LA FORMULACIÓN DEL EC-2 PARA LA RESISTENCIA A CORTANTE EN VIGAS DE HORMIGÓN ESTRUCTURAL SIN ARMADURA
-> Mejora de la formulación del EC-2 para la resistencia a cortante en vigas de hormigón estructural sin armadura transversalArtículo presentado en el Congreso internacional titulado ”V Congreso Internacional de estruturas – ACHE 2011” celebrado del 25 al 27 de outubre de 2011 en Barcelona, España
5.2 REGRESIÓN SIMBÓLICA EN INGENIERÍA CIVIL MEDIANTE TÉCNICAS DE PROGRAMACIÓN GENÉTICA
-> Regresión simbólica en Ingeniería Civil mediante técnicas de Programación GenéticaArtículo presentado en el VIII congreso español sobre Metaheuristicas, Algoritmos Evolutivos y Bioinspirados – MAEB 2012 celebrado del 8 al 10 de febrero de 2012 en Albaceta, España
5.3 GENETIC PROGRAMMING TO IMPROVEMENT FIB MODEL: BOND AND ANCHORAGE OF REINFORCING STEEL IN STRUCTURAL CONCRETE
-> Genetic Programming to Improvement FIB ModelArtículo presentado en el Congreso internacional titulado ”International Work Conference on Artificial Neural Networks – IWANN2013”” celebrado del 12 al 14 de junio de 2013 en Tenerife, España.
6 BIBLIOGRAFÍA
Arciszewski, T., & De Jong, K. A. (2001). Evolutionary computation in civil engineering: research frontiers. In B. H. V. Topping (Ed.), Proceedings of the Eight International Conference on Civil and Structural Engineering Computing, Eisenstadt, Vienna, Austria.
Kicinger, R., Arciszewski, T. and De Jong, K.(2005). Evolutionary computation and structural design: A survey of the state-of-the-art. Computers and Structures, 83, 1943–1978.
McCulloch, W. S., & Pitts, W. (1943). A Logical Calculus of Ideas Immanent in Nervous Activity”. Bulletin of Mathematical Biophysics, 5, 115-133.
Wasserman, P. D. (1989). Neural Computing. New York: Ed. Van Nostrand Reinhold.
Brown, M., & Harris, C.(1994). Neurofuzzy adaptive modelling and control. Prentice-Hall
Lin, C.T., & Lee, C.S., (1996). Neural Fuzzy Systems: A neuro-fuzzy synergism to intelligent systems. Prentice-Hall.
Hoskins, J.C., & Himmelblau, D.M. (1992 ). Process control via artificial neural networks and reinforcement learning. Computers & Chemical Engineering, 16(4), 241-251.
Darwin, C. (1859). On the origin of species by means of natural selection or the preservation of favoured races in the struggle for life. Cambridge, UK:Cambridge University Press.
Darwin, C & Wallace, A. R. “On the Tendency of Species to form Varieties; and on the Perpetuation of Varieties and Species by Natural Means of Selection”. Journal of the Proceedings of the Linnean Society of London. Zoology 3: 46-50. 1858.
Holland, J.H.(1975). Adaptation in natural and artificial systems. Ann Arbor, MI: University of Michigan Press.
Gandson, L.A. (2005) Taylor n-dimensional nets, The analytic equivalence to Neural Nets, University Press of Kentucky.
Ahmet Öztaş et al. Predicting the compressive strength and slump of high strength concrete using neural network. Construction and Building Materials 20, 769 – 775. 2006
Rabuñal, J.R. Entrenamiento de Redes de Neuronas Artificiales mediante Algoritmos Genéticos. Graduate Thesis, Facultad de Informática, University of A Coruña, Spain. 1999.
Rodríguez, I. Study of concrete dosages using artificial neuronal network trained with genetical operators. A Coruña, Spain. 2002.



No hay comentarios:
Publicar un comentario