3 Development and improvement of theoretical models of structural concrete from its dosage by genetic programming and artificial neural networks / Desarrollo y mejora de modelos teóricos del hormigón estructural a partir de su dosificación mediante técnicas de programación genética y redes de neuronas artificiales

Investigación de Enmacosa dentro del proyecto "Desarrollo y mejora de modelos teóricos del hormigón estructural a partir de su dosificación mediante técnicas de programación genética y redes de neuronas artificiales", cofinanciado por la Xunta de Galicia (2010-2013). 

Enmacosa research within the project "Development and improvement of theoretical models of structural concrete from its dosage by genetic programming and artificial neural networks", cofinanced by the Xunta de Galicia (2010-2013).

Continúa de: http://carreteras-laser-escaner.blogspot.com/2014/12/2-development-and-improvement-of.html

1 Introducción. 
2 Seguimiento - Finalización. 
3 método aplicado. 
   3.1 Fase 1. Identificación de variables clave ..
   3.2 Fase 2. Análisis de los resultados
   3.3 Fase 3. Aplicación de técnicas de regresión .
4 Resultados alcanzados. 
   4.1 Base de datos 
      4.1.1 Resultados. 
      4.1.2 Caracterización de base de datos
   4.2 Variables que afectan a las propiedades del hormigón.
      4.2.1 Las variables con alta influencia.
      4.2.2 Variables que influyen en los medios de comunicación.
      4.2.3 Variables con baja influencia.
   4.3 Aplicación de RR.NN.AA.  la predicción de parámetros físicos medibles mediante ensayos 
   4.4 Análisis de la resistencia alcanzado por los diferentes hormigones, en relación con la especificada
   4.4.1 Análisis por el fabricante
   4.5 Análisis de consistencia obtenidos con respecto como se especifica
   4.6 Análisis de la evolución de la resistencia del hormigón con la edad
      4.6.1 CEM I 52,5 R
      4.6.2 CEM II 42.5 R
      4.6.3 I / 52,5 N / SR
      4.6.4 III / A 42,5 N / SR
      4.6.5 IV / A-V 42,5 N / SR.
   4.7 Análisis de la relación y el contenido de agua / cemento con la resistencia del hormigón.
   4.8 Predicción del módulo del hormigón - Convencional
5 Publicaciones.
   5.1 Mejora de la formulación de la EC-2 para la resistencia al corte en vigas de hormigón Estructural sin armadura.
   5.2 Regresión simbólico en Ingeniería Civil a través de técnicas de programación genética. 
   5.3 Programación Genética para Modelo de Mejora FIB: Bond y Anchorage de refuerzo Acero Estructural en Concrete
6 Bibliografía

4.4 ANÁLIS DE LA RESISTENCIA ALCANZADA POR LOS DIFERENTES HORMIGÓNS, EN RELACIÓN CON LA ESPECIFICADA

La norma española exige cumplir a cada lote de hormigón una resistencia específica, determinada por lo general a los 28 días de la. El método empleado en la rotura de probeta normalizadas, cuyo resultado es la resistencia media. Esta resistencia no es exactamente la característica dado que esta última de asociarse al percentil del 95%. Es decir cuando la defensa característica e indica un valor X se considera que el 95% del material debe superar ese valor. La norma española admite una distribución normal de los resultados de resistencia, y marca la resistencia característica con un valor que dista -1.64d de media (d es la desviación estándar). Por otra parte, de acuerdo a los datos tradicionalmente considerados, la distancia entre la resistencia característica y la media se sitúa en 8 MPa. ¿Este dato es cierto? Se puede comprobar a partir de la base de datos.

Se seleccionan de la base de datos o los ensayos a 28 días correspondientes a diferentes resistencias especificadas (características). Previsiblemente, los resultados de laboratorio deben de tener una distribución no centrada en el valor característico, y probablemente de tipo normal.

Los resultados alcanzados se presentan resumidos en la tabla Táboa 8 para resistencias de valor 25, 30, 35 40, 45, 50 e 70 MPa.

De forma gráfica se presentan los programas. Con la curva normal de vida de los datos experimentales. Con los datos se determina la resistencia media del conjunto y la desviación estándar, parámetros con los que se representa una distribución normal asociada. En ella se fija el valor característico. Simultáneamente, a partir de la función real de los datos se calcula la distribución acumulada, y se calcula el pretendiente 5% real. En este momento se puede comparar la distribución real con la teórica.

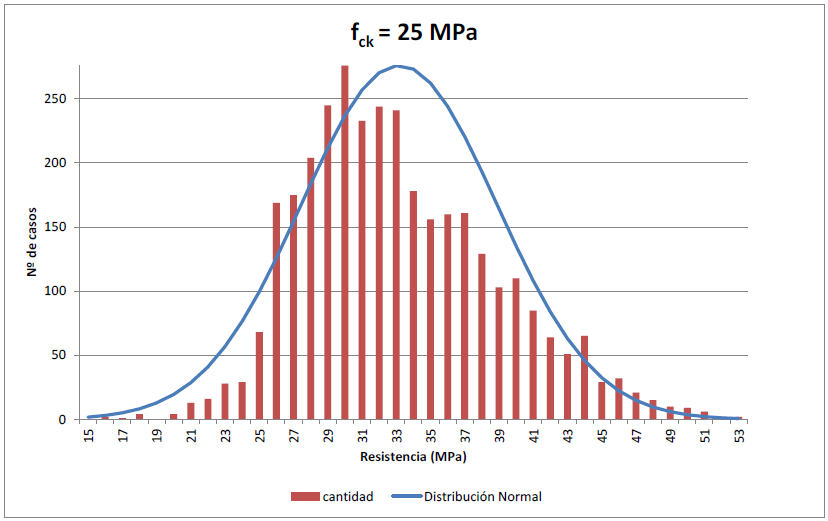Figura 10. Resistencia alcanzada para el grupo de fck = 25 MPa

Figura 11. Resistencia alcanzada para el grupo de fck = 30 MPa

Figura 12. Resistencia alcanzada para el grupo de fck = 35 MPa

Figura 13. Resistencia alcanzada para el grupo de fck = 40 MPa

Figura 14. Resistencia alcanzada para el grupo de fck = 45 MPa

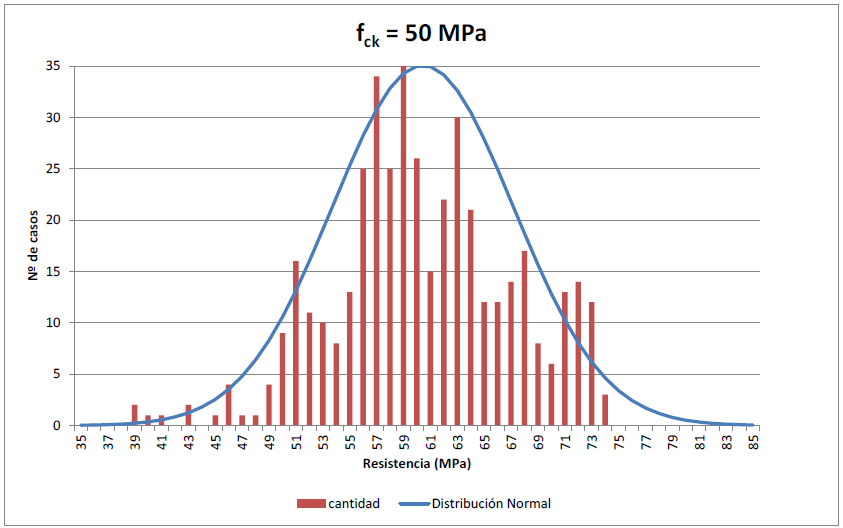Figura 15. Resistencia alcanzada para el grupo de fck = 50 MPa

Figura 16. Resistencia alcanzada para el grupo de fck = 70 MPa

En conclusión, se puede observar el buen cumplimiento de las exigencias por parte de los hormigones analizado. Los datos o menos fiables en la resistencia del 45, 50 e 70 MPa por tener menos datos. No obstante, por cumplir la exigencia resistente, el valor de 8 MPa proporciona seguridad.

4.4.1 Análisis por fabricante

A continuación se estudia por cada fabricante la resistencia alcanzada frente a la especificada. En esta ocasión se selecciona el conjunto con resistencia especificada de 30 MPa por ser la que dispone de más ensayos.

Cabe destacar que los resultados que se muestran en casi todos los fabricantes aglutinaron todos varias plantas de fabricación.

Figura 17. Resistencia alcanzada por el Fabricante 1. 

Figura 18. Resistencia alcanzada por el Fabricante 2

4.5 ANÁLISIS DE LA CONSISTENCIA ALCANZADA EN RELACIÓN CON LA ESPECIFICADA

Una de las comprobaciones que se hacen en obra es recibir el hormigón y cualificar la consistencia (seca, plástica, blanda e fluida) mediante el ensayo denominado “cono de Abrams” Con el cálculo, tras un proceso normalizado, se mide la disminución de la altura con respecto al molde único. Con esta altura y empleando la tabla 10 Se cuantifica en tipo de consistencia.

De esta forma la Dirección Facultativa podrá recibir el hormigón tras comprobar si se encuentra en el intervalo solicitado.

Figura 22. Consistencia blanda

Figura 23. Consistencia fluida

Figura 22. Consistencia líquida

La lectura del cono de la tabla superior se determinan mediante el siguiente código:

4.6 ANÁLISIS  DE LA EVOLUCIÓN DE LA RESISTENCIA DEL HORMIGÓN CON LA EDAD

La norma española establece una fórmula experimental para predecir el valor de la resistencia edades diferentes de los 28 de esta fórmula de tipo exponencial, y propone multiplicada presencia a los 28 días por un factor b:

donde t es la edad en días e s es un parámetro que toma los valores 0.2 (cementos de endurecemento rápido), 0.25 (cementos de endurecemento normal) e 0.38 (cementos de endurecemento lento).

La base de datos proporciona numerosos datos con resistencias a 7, 28 e 90 días. Estos datos se analízan y se compáran con los proporcionados por la ecuación anterior.

El procedimiento empleado, en primer lugar en un trabajo relevante sobre la base de datos.  Se seleccionó un conjunto de cemento de los que se disponen datos suficientes. Los elegidos son: CEM I 52.5 R, CEM II42.5 R, I 52.5 N SR, III 42.5 N SR , y IV A-V 42.5 N SR. A estos eventos se recogen todos las roturas en las edades indicadas para cada masada controlada. Sólo son aprovechables las series con las tres edades de ruptura, perdiéndose por eso algunos datos que sólo cuentan con una o dos edades. A continuación se calculan los datos y se tabulan los factores fc(7días)/fc(28 días) e fc(90

días)/fc(28 días). Los resultados se comparan con factores que proporcionan la ecuación, se muestran a continuación.

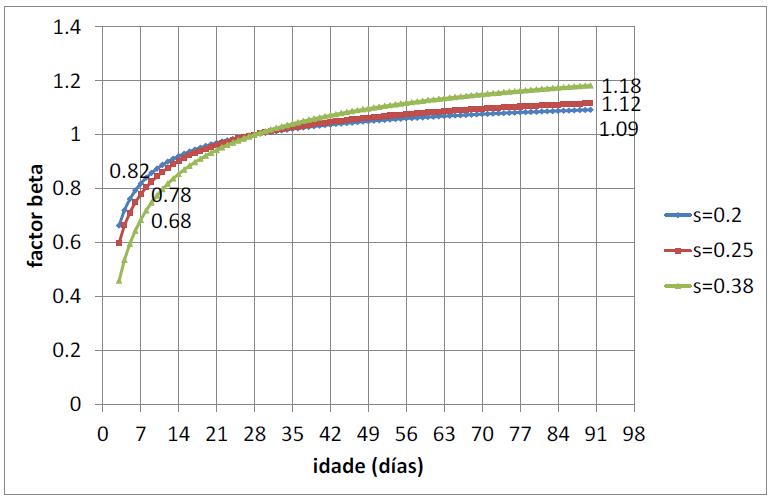Figura 25. Evolución de los factores con la edad

4.6.1 CEM I 52.5 R

Se analizan 4582 datos. La distribución se muestra la gráfica adjunta.

Figura 26 . Factor beta a 7 y 90 días del CEM I 52.5R

No es una distribución normal, en contra de lo previsto. El valor promedio del factor b (7 días) es de 0.85 y de 1.11 para b (90 días).

4.6.2 CEM II 42.5 R

Se analizaron 912 datos. La distribución se distribuye según la gráfica adjunta.

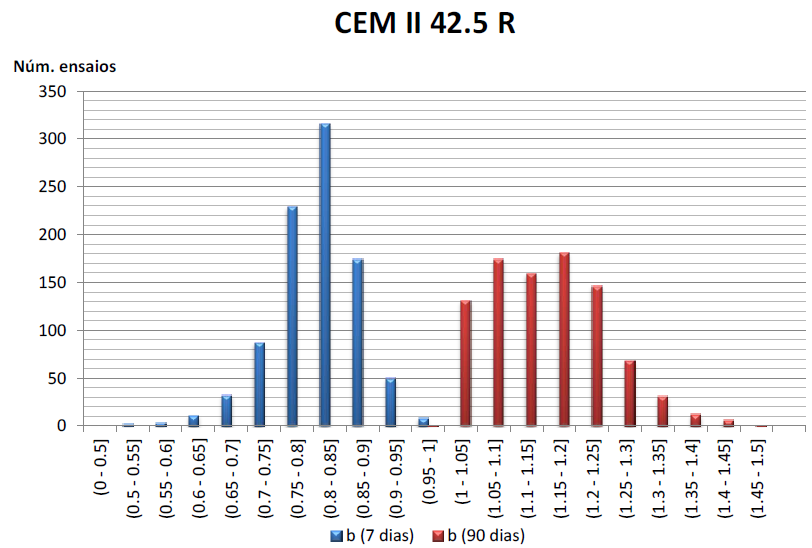Figura 27. Factor beta a 7 y 90 días del CEM II 42.5 R

La distribución no es normal en el caso de siete días y muy variable en el caso de 90 días. El valor promedio del factor b (7 días) es de  0.81 y de 1.15 para b (90 días).

4.6.3 I/52.5 N/SR

Se analizaron 1.724 datos. La distribución se distribuye según la gráfica adjunta.

Figura 28. Factor beta a 7 y 90 días del I/52.5 N/SR

La distribución es aproximadamente normal en los dos casos, pero dispersa en el caso de siete días. El valor promedio del factor  b (7 días) es de  0.81 y de 1.08 para b (90 días).

4.6.4 III/A 42.5 N/SR

Se analizaron 943 datos. La distribución se distribuye según la gráfica adjunta.

Figura 29. Factor beta a 7 y 90 días del III/A 42.5 N/SR

La distribución es aproximadamente normal en los dos casos, pero dispersa en el caso de siete días. El valor promedio del factor  b (7 días) es de  0.63 y de 1.16 para b (90 días).

4.6.5 IV/A-V 42.5 N/SR

Se analizaron 943 datos. La distribución se distribuye según la gráfica adjunta.

Figura 30. Factor beta a 7 y 90 días del IV/A-V 42.5 N/SR

La distribución es aproximadamente normal en los dos casos, pero dispersa en el caso de siete días. El valor promedio del factor  b (7 días) es de  0.79 y de 1.20 para b (90 días).

Ateniéndonos fuertemente analizados, cabría esperar que el CEM I 52.5R y el CEM II 42.5 R se debían adaptar al factor s = 0.2. Esta tradición es correctamente en el caso pero no en el segundo. El cemento I 52.5 N SR debería adaptarse al caso s = 0.25, y no es cierto.

A la vista de los resultados y del número de casos, se aplican técnicas simples de algoritmos genéticos para generar una ecuación que se adapte a los cinco casos. Para eso se permite modificar la técnica de exploración de las dos constantes de la fórmula de la norma (el valor de s y el coeficiente del exponente del término (28/t).)

Se introduce como ecuación de partida la siguientes:

Los mejores resultados son los siguientes:

Atendiendo esta última tabla y si nos fijamos en el tipo de endurecimiento los valores de K1 y K2  Se podrían establecer los valores que vemos en la tabla siguiente. Cabe resaltar que no consideramos el cemento IV/A-V 42.5 N/SR para el cálculo de los coeficientes para el endurecimiento normal (N) ya que los valores obtenidos por K1 y K2 Son más dispares comparados con los de su grupo.

No se considera que los resultados eran un patrón consistente, por lo que analizar el problema desde otra perspectiva, es decir, aceptando el exponente 0.5 y variando sólo el valor de s. El mejor resultado es el siguiente:

Atendiendo hasta última tabla y si nos fijamos en el tipo de crecimiento los valores de K1 (s) se podrían establecer con los siguientes coeficientes:

4.7 ANÁLISIS DE LA RELACIÓN Y DEL CONTENIDO AGUA/CEMENTO CON LA RESISTENCIA DEL HORMIGÓN

Continua en: http://carreteras-laser-escaner.blogspot.com/2014/12/4-development-and-improvement-of.html