Solving complex type functions / Solución de funciones de tipo complejo

Detrás de la simple ecuación del esponente del número "e" a un número complejo:

Behind the simple equation of the exponent of the number "e" to a imaginary number:

e^{( a + bi )} = e^a · Cos(b) + [e^a · Sen(b)]i

Y dando un poco de vueltas a las propiedades de las funciones trigonométricas, la exponencial y el logaritmo. Se llegan con cierta "facilidad" a las soluciones complejas de las funciones siguientes:

And studying the properties of trigonometric functions, exponential and logarithm. We easily get imaginary solutions of the following functions:

Sen( a + bi ) = Sen(a) · Ch(b) + [Cos(a) · Sh(b)]i

Cos( a + bi ) = Cos(a) · Ch(b) + [Sen(a) · Sh(b)]i

Tan( a + bi ) = Tan(a) · (1-Th²(b)) / (1+Tan²(a) · Th²(b) ) +                    + [Th(b) · (1+Tan²(a)) / (1+Tan²(a) · Th²(b) )]i

Log_n( a + bi) = Ln(a²+b²)/(2Ln(n)) + [Atn(b/a) /Ln(n)]i

( a + bi )^{( c + di )} = e^f · Cos(g)+ e^f · [Sin(g)]i

Donde: Where:

           f = c·Ln(√(a²+b²)) - d·Atn(b/a)

           g = c·Atn(b/a) + d·Ln(√(a²+b²))

Sh( a + bi ) = Sh(a) · Cos(b) + [Ch(a) · Sen(b)]i

Ch( a + bi ) = Ch(a) · Cos(b) + [Sh(a) · Sen(b)]i

Este tema es muy escueto pero para mi es un recordatorio obligado cuando me sumerjo en cálculos de tipo complejo.

This topic is very brief but to me is a compelling reminder when I need to calculate with imaginary number.

Regresión simbólica en Ingeniería Civil mediante técnicas de Programación Genética

Artículo patrocinado por Enmacosa dentro del proyecto "Formigón estructural", cofinanciado por la Xunta de Galicia (2013). 

Autores: Alba Catoira, Juan Luis Pérez, Juan R. Rabuñal y Fernando Martínez-Abella

Resumen

 El objetivo principal que se presenta en este artículo es mostrar las virtudes del empleo de la Programación Genética (GP) como herramienta en la extracción de conocimiento de datos experimentales. El ejemplo elegido para ello se enmarca dentro del ámbito de la Ingeniería Civil.

Se presenta pues, un sistema de Programación Genética Distribuida que aplica un algoritmo de clustering para alcanzar soluciones más heterogéneas. La finalidad del sistema es la de extraer fórmulas matemáticas (regresión simbólica) a través de un conjunto de datos de entrada y sus correspondientes salidas utilizando para ello una versión distribuida del método de Programación Genética clásico. La distribución del algoritmo permite disminuir considerablemente el número de pruebas necesarias para alcanzar una solución óptima, disminuyendo a su vez el coste humano y de recursos asociado.

I. INTRODUCCIÓN

En el ámbito de la Ingeniería Civil, al igual que en otras disciplinas, se requiere predecir el comportamiento de determinados materiales o estructuras en función de diversas condiciones de contorno que influyen su comportamiento teórico. Es aquí, tras la experiencia adquirida en los ensayos de laboratorio y materializada en conjuntos de datos que relacionan entradas con salidas reales, donde la Programación Genética (PG) [1] resulta de gran utilidad puesto que permite realizar regresión simbólica sobre un conjunto de datos experimentales. La PG es una técnica de búsqueda inherentemente paralela que requiere gran cantidad de cálculos complejos. Dicha complejidad hace que la distribución de los cálculos sea de gran utilidad.

Es por ello que se ha propuesto que el sistema desarrollado sea distribuido, permitiendo así reducir el tiempo de cálculo. En este contexto, cuando el espacio de búsqueda es amplio y complejo, es común obtener procesos evolutivos que lleven a mínimos locales. Por este motivo, en este trabajo se utiliza una ejecución paralela del algoritmo mediante varias poblaciones que intercambian individuos entre ellas, aumentando la heterogeneidad.

El sistema desarrollado denominado “DistClustPG” [2] aplica un algoritmo de clustering [3] [4] para dividir cada población en grupos de acuerdo a una medida de similitud. A continuación, se eligen los representantes de cada grupo para formar parte del proceso de migración entre poblaciones consiguiendo así, además de la distribución del cómputo, una estrategia co-evolutiva.

II. SISTEMA DISTRIBUIDO DE PROGRAMACIÓN GENÉTICA

El DistClustPG está basado en la ejecución paralela del algoritmo de PG sobre poblaciones independientes o porciones de una sola población. Cada población evoluciona localmente mediante el algoritmo PG de forma independiente, y contribuye a la evolución total del sistema a través de un intercambio periódico de individuos. 

En la PG clásica puede ocurrir que un individuo (fórmula matemática) tenga un valor de fitness óptimo y, sin embargo, que su estructura sea demasiado compleja para la posterior interpretación por parte de los expertos (en este caso en Ingeniería Civil), o bien que dos individuos con el mismo valor de fitness sean estructuralmente muy diferentes. Es por ello que tras un número de generaciones previamente establecido por el experto, cada nodo aplica el algoritmo de clustering sobre su población, dividiéndola en grupos según una medida de similitud. Dicha medida de similitud mide la distancia entre un individuo (representado en forma de árbol) y el árbol vacío. De este modo, se crean grupos según el nivel de complejidad estructural de los individuos. Una vez creados los grupos, se elige a los representantes de los mismos (el de mejor valor de fitness) y estos representantes son los que forman parte del proceso de migración. 

Cada nodo envía sus representantes al nodo maestro, que a su vez, los incorpora a su propia población, y aplica el algoritmo de PG sobre ellos, haciéndolos evolucionar. Tras un número de generaciones preestablecido, el nodo maestro aplica su algoritmo de clustering sobre la población evolucionada, y envía sus representantes a todos los nodos del sistema. 

A. Arquitectura de DistClustPG

El entorno básico en el que se utiliza el sistema es una red Ethernet de ordenadores. DistClustPG está constituido por un nodo maestro y una serie de nodos denominados esclavos, de acuerdo con el esquema de arquitectura típico maestro-esclavo. El nodo principal o maestro es el que gestiona la ejecución de los nodos esclavos y almacena los resultados obtenidos en los mismos. Es también el responsable de enviar a los demás nodos las órdenes y los datos necesarios para la ejecución (parámetros, patrones, etc.). Los esclavos poseen el algoritmo PG y el algoritmo de clustering para poder evolucionar su población. 

Tras un número prefijado de generaciones, los nodos aplicarán el algoritmo de clustering, agrupando a los individuos de la población actual en grupos de acuerdo a una medida de similitud. Posteriormente, eligen a los representantes de cada grupo y se los envían al nodo maestro, que posee su propia copia del algoritmo PG y de clustering, y que hará evolucionar a su vez los individuos recibidos de los esclavos. En todo este proceso anteriormente descrito, los nodos sólo detienen su ejecución de PG para aplicar el algoritmo de clustering. Es entonces cuando incorporan a su población aquellos individuos que han recibido de otros nodos (almacenados temporalmente en un buffer). De este modo, se obtiene un mayor rendimiento. La Figura 1 muestra el diagrama de secuencia del funcionamiento de la arquitectura DistClustPG.

Fig. 1. Diagrama de secuencia

Donde d(R1,R2) = | key(R1)-key(R2)|, y key es una función de codificación que asigna un valor numérico a cada nodo en el árbol según su tipo, childi(Y) es el iésimo hijo de los m posibles del nodo Y si i≤m o el árbol vacío en otro caso. La constante K se usa para dar diferentes pesos a los nodos según su nivel de profundidad en el árbol. En caso de calcular la distancia entre un árbol y el árbol vacío, el resultado sería la suma de las claves del árbol ponderadas por su nivel de profundidad. 

Supongamos el siguiente árbol (representado en la Figura 2):

Fig. 2. Un ejemplo de árbol.

En la siguiente tabla, se muestran los valores asociados a cada uno de los nodos. Estos valores han sido establecidos mediante experimentación, y de forma que las claves entre operadores de un mismo grupo sean más similares que entre grupos.

TABLA I CLAVES DE LOS OPERADORES

La distancia entre el árbol anterior y el árbol vacío vendría determinada por la ecuación (3).

Los individuos de la población son ordenados en base a la distancia al árbol vacío, y se crean grupos teniendo en cuenta un valor umbral, que se recalcula en cada ejecución del algoritmo. El experto establece el máximo porcentaje de clusters que desea crear en función del tamaño de la población y el umbral se calcula como se muestra en la ecuación (4).

donde dmax y dmin son la máxima y mínima distancia al árbol vacío en la población, respectivamente, y max número de clusters desscrita en la ecuación (5).

Para crear los clusters, se toma como referencia el primer individuo de la población ordenada, y estarán en el mismo grupo aquellos individuos cuyas distancias al árbol vacío no superen el umbral. Si esta condición no se cumple para un individuo, éste se convierte en el nuevo elemento de referencia y se crea un nuevo grupo.

Una vez se hayan clasificado todos los individuos, se ordena internamente cada grupo según el valor de ajuste, y se elige al de mejor fitness como representante. Si el resultado del proceso de clustering fue la creación de k clusters, habrá k representantes, que se enviarán al nodo maestro para formar parte de su población.

Al igual que los esclavos, el nodo maestro aplicara el algoritmo PG sobre los individuos recibidos, aplicará el algoritmo de clustering y enviará a los esclavos sus propios representantes.

III. RESULTADOS EXPERIMENTALES

El hormigón de altas prestaciones (HPC: High-Performance Concrete) constituye una evolución muy empleada en la industria de la construcción con hormigón. Además de los tres componentes básicos del hormigón convencional, que son el cemento, los áridos (finos y gruesos) y el agua, la elaboración de HPC incorpora adiciones como cenizas volantes (fly ash), escoria del horno (blast fumace slag) y aditivos químicos como fluidificantes, aceleradores y retardadores de fraguado…[9] [10]. El HPC es un material altamente complejo, lo que implica que conocer a priori el comportamiento del hormigón dados los materiales empleados resulta una tarea no resuelta. 

El índice de Abrams o la relación agua-cemento (w/c) conocido en 1918 [11] Constituye, junto a la cantidad de cemento, el índice más significativo de la mezcla de hormigón ya que se encuentra en relación inversamente proporcional a la resistencia del hormigón [12]. La relación a/c y la cantidad de cemento determinan, pues, junto al resto de componentes, la resistencia final que presentará una muestra de hormigón. En la actualidad no existe una formulación ni analítica ni empírica que prediga la resistencia del hormigón a partir de sus componentes, a pesar de la existencia de series de datos extensas. Contar con ella, sin lugar a dudas, supondría un importante avance en el conocimiento [13].

Una vez presentado el problema, se detallan las soluciones al mismo comparando los resultados de la aproximación clásica de Programación Genética con el nuevo sistema desarrollado de Programación Genética distribuida. Por otro lado, se compara el resultado del sistema distribuido con otras aproximaciones [14], [15]. 

El conjunto de datos utilizado se ha obtenido de la base de datos del UCI Learning Repository [16]. El problema consta de 8 variables de entradas de tipo real: cemento(c), el agua (w), la escoria (sl), la ceniza volante (fl), el superplastificante (sp), el árido grueso (ca), el árido fino (fa) y la edad de ensayo (age). Se han empleado 720 patrones de entrada para la fase de entrenamiento y 308 patrones para la fase de test. En la Tabla 2 pueden verse los rangos de valores típicos para las variables que utilizarán ambos sistemas. La salida es la resistencia del hormigón a la compresión, de la que se pretende conseguir una expresión matemática que modele el comportamiento real para el caso del HAP. 

A. Comparación con la PG clásica

Continúa en: http://carreteras-laser-escaner.blogspot.com/2014/12/regresion-simbolica-en-ingenieria-civil.html

Genetic Programming to Improvement FIB Model II / Programación Genética para el Mejoramiento del Modelo FIB II

Artículo patrocinado por Enmacosa dentro del proyecto "Formigón estructural", cofinanciado por la Xunta de Galicia (2013). 

Article sponsored by Enmacosa inside the "Formigón estructural" project, cofinanced by the Xunta de Galicia. (2013)

Adherencia y Anclaje de acero de refuerzo en Hormigón Estructural / Bond and Anchorage of Reinforcing Steel in Structural Concrete

Continue from: http://carreteras-laser-escaner.blogspot.com/2014/11/genetic-programming-to-improvement-fib.html

3 Método / Method

El método seguido se orienta a la mejora de las ecuaciones FIB desarrollados para la predicción de la tensión de la barra de anclado. El método utilizado sigue las mismas directrices mencionadas en el documento elaborado por Pérez [7]. En resumen, el método se basa en técnicas de GP imponiendo algunas restricciones basadas en el conocimiento del problema proporcionadas por un experto. Los datos de regresión simbólica son una de las capacidades proporcionadas por el GP..

The method followed is oriented to improving the FIB equations developed for predicting the stress of bar anchored. The method used follows the same guidelines referred to in the paper developed by Pérez et al [7]. In summary, the method is based on GP techniques, imposing some restrictions based on knowledge of the problem provided by an expert. Symbolic regression data is one of the capabilities provided by the GP.

Disponiendo de un conjunto de datos (input-output), el GP es capaz de relacionar estos datos con una ecuación algebraica. Su complejidad puede variar, y la integridad dimensional no está garantizada. Esta técnica, aplicada en muchos casos en ingeniería civil, es uno de los seguidos por Ashour [8], por ejemplo, para predecir la resistencia a la cortante en vigas de hormigón. Naturalmente, la forma de las ecuaciones obtenidas es muy diferente de las de los códigos comunes. El método presentado mejora los términos aceptados por la comunidad científica, conseguir un mejor ajuste cuando los resultados se aplican a una base de datos.

Having a data set (input-output), the GP is able to relate these data algebraically by an equation. Its complexity may vary, and dimensional integrity is not guaranteed. This technique, applied in many cases in civil engineering, is one of those followed by Ashour al [8], for example, to predict shear strength in concrete beams. Naturally, the form of the equations obtained is very different from the ones in the common codes. The presented method improves the terms accepted by the scientific community, getting a better fit when the results are applied to a database.

Se parte de la expresión FIB-2006, ya que muestra mejores resultados en la base de datos. La expresión de búsqueda determinará la resistencia predicha de la probeta (Spred) al compararse con la prueba de esfuerzo real (σtest). En primer lugar, es necesario definir cómo se evaluarán los elementos individuales en la función de aptitud (ecuación 4). En esta ecuación, σtest es la tensión de barra en la rotura, α es el coeficiente de retraso, si es el número de nodos en la expresión y n es el número de casos de la base de datos. Se deben establecer los parámetros pi y lbias definidos en la ecuación 3.

Después de realizar varias pruebas, fue adoptado lbias = 1,0, y la ecuación 4 muestra el valor de pi (DP). Esta ecuación se basa en el uso de la técnica de "puntos fijos".

It starts from the expression FIB-2006, because it shows better results over the database. The search expression will determine the bar stress predicted (spred) to be compared with the real stress test (σtest). Firstly, it is necessary to define how individuals will be evaluated in the fitness function (equation 4). In this equation, σtest is the bar stress at failure, α is the parsimony coefficient, si is the number of nodes in the expression and n is the number of cases of the database. It should set the parameters pi and lbias defined in equation 3.

After performing several tests, was adopted lbias = 1.0, and equation 4 shows the value of pi (DP). This equation is based on the use of the technique of "demerit points".

La técnica se adaptó para que las búsquedas "orientadas" fueran posibles, con diferentes propósitos.

La orientación se introdujo a través de imposiciones ni restricciones, que incluyen:
─ Restricción sobre el tipo de funciones que vinculan las variables
─ Selección preferida de los elementos con el más alto proporciones σtest / σpred. Desde el punto de vista estructural, es mucho más apropiado esta opción por razones de seguridad

El método utilizado se inicia con el establecimiento de un "marco" de la programación genética que hará que el proceso evolutivo tenga en cuenta las restricciones e imposiciones.

El marco se define directamente de la ecuación FIB-2006, que se divide en subexpresiones. Además, cada subexpresión está escrita para que los factores (rama) puede cambiar en el proceso de búsqueda. Las líneas de trabajo que se pueden encontrar son:
─ La optimización de los coeficientes numéricos de la ecuación. Las ramas serán valores reales
─ La introducción de una nueva sub-expresión. Esto puede ser un número real o una función (nueva rama) vinculado a una variable

Como se ha mencionado, en este tipo de modelo es muy importante que el estrés predicho es igual o mayor que el valor real.

En general, si un individuo se diferencia del valor real está penalizado durante el entrenamiento. Desde un punto de vista matemático, S valora igual a 0.5 o 1.5 debe ser penalizado por igual. Para tener en cuenta la seguridad estructural, el individuo 0.5 debe ser penalizado más que el individuo 1,5, ya que causa la inseguridad estructural (colapso).

Esto se logra mediante la técnica de puntos fijos, con lo cual se pondera el error de la expresión de acuerdo con los rangos definidos por Pérez [9]. La función de aptitud (3) muestra cómo los pesos del factor pi el error de predicción, de acuerdo con los intervalos y valores de la ecuación (4).

El método utilizado se inicia con el establecimiento de un "marco" sobre el que la programación genética hará que el proceso evolutivo, teniendo en cuenta las restricciones e imposiciones. Tal "marco" se basa en la formulación de FIB 2006, sobre la que se va a introducir nuevas variables o sus coeficientes se modificará.

En el proceso de búsqueda se ha propuesto tres ecuaciones básicas (5) (6) (7). Cada rama se designa como Bi. La Tabla 3 muestra los valores predeterminados en práctica, sobre la base de las pruebas iniciales. Los datos de entrada no se han normalizado, por lo que las expresiones se pueden utilizar directamente.

The technique was adapted for “oriented” searches were possible, with different purposes. 

The orientation was introduced through impositions or restrictions, which include:

─ restriction on the type of functions that link the variables

─ preferred selection of individuals with the highest ratios σtest/σpred. From the structural point of view, is much more appropriate this option for safety reasons 

The method used starts with the establishment of a “framework” from wich genetic programming will make the evolutive process, taking into account the restrictions and impositions.

The framework is defined directly from the equation FIB-2006, which is divided into subexpressions. Also, each subexpression is written indicating which factor (branch) may change in the search process. The working lines can find:

─ The optimization of the numerical coefficients of the equation. The branches will be Real values

─ The introduction of a new subexpression. This can be a Real number or a function (new branch) linked to a variable

As mentioned, in this type of model is very important that the predicted stress is equal to or greater than the actual value.

In general, if an individual differs from the real value is penalized during training.

From a mathematical point of view, S values equal to 0.5 or 1.5 should be penalized equally. To take into account the structural safety, the individual 0.5 should be penalized more than the individual 1.5, as it causes structural insecurity (collapse).

This is achieved through the technique of demerit points, whereby the error of the expression is weighted according to the ranges defined by Pérez [9]. The fitness function (3) shows how the pi factor weights the prediction error, according to the intervals and values of the equation (4).

The method used starts with the establishment of a “framework” about whom genetic programming will make the evolutive process, taking into account the restrictions and impositions. Such “framework” is based on the 2006 FIB formulation, about which it will be introduced new variables or its coefficients will be modified.

In the searching process it has been proposed three basic equations (5)(6)(7). Each branch is designated as Bi. Table 3 shows the default settings implemented, based on the initial tests. The input data have not been standardized, so expressions can be used directly.

Table 3. Parameters used

Por defecto, la suma, resta, multiplicación y división protegida fueron elegidos como operadores o nodos no terminales. Las variables del conjunto de datos (ls, db, cmin, cmax y fc), y números enteros en el rango [-10, 10] fueron adoptados como los nodos terminales.

Las restricciones sobre las ecuaciones se muestran en la tabla 4. Para la ecuación (5) se han impuesto tres tipos de restricciones ("A", "B" y "C"), la restricción de "D" a la ecuación (6) y, finalmente, la restricción "se impone E "a la ecuación (7).

By default, addition, subtraction, multiplication and protected division were chosen as operators or non-terminal nodes. Variables from the data set (ls, db, cmin, cmax and fc), and integers in the range [-10, 10] were adopted as terminal nodes.

Constraints over the equations are showed in table 4. Equation (5) have three types of constraints (“A”, “B” and “C”), the constraint “D” is imposed to equation (6) and finally the constraint “E” is imposed to equation (7).

Table 4. Constraints

4 Results

En total, más de 4.500 ejecuciones se llevaron a cabo. Los resultados se analizan fundamentalmente a través de los siguientes indicadores: COV (coeficiente de variación), σtest / σpred, R2 (raíz cuadrada de Coeficiente de correlación de Pearson), MSE (media de error de raíz cuadrada), ME (error de decir), y finalmente demérito puntos calculados según la ecuación (4).

De acuerdo con los mejores resultados, se optó por un selecto grupo de ecuaciones. Si el denominador fuera negativo, las expresiones que contienen "división protegida" fueron rechazadas. Además también se descartaron ecuaciones demasiado complejas.

PG_9RSC4 (8), PG_8v2R5 (9), PG_7v3F2 (10), PGcc6 (11) eran ecuaciones más precisas. Dado que no proporcionan mejoras sustanciales, estas ecuaciones no contienen los derivados de la GP clásico. Los resultados se muestran en la Tabla 5. La mejora significativa logrado es evidente mediante la comparación de los resultados de la FIB ecuaciones.

In total, more than 4,500 executions were carried out. The results are analyzed essentially through the following indicators: COV (variation coefficient), σtest/σpred , R2 (square root of Pearson product-moment correlation coefficient), MSE (mean square root error), ME (mean error), and finally demerit points calculated according to equation (4).

According to the best results, a select group of equations was chosen. If the denominator could be negative, expressions containing function "protected division" were rejected. Also too complex equations were also discarded.

PG_9RSC4 (8), PG_8v2R5 (9), PG_7v3F2 (10), PGcc6 (11) were more accurate equations. Since not provide substantial improvements, these equations do not contain the derivatives of the classic GP. The results are shown in Table 5. The significant improvement achieved is evident by comparing the results of the equations FIB.

Table 5. Results

Algunas de las expresiones destacan por diferentes aspectos. PG_9RSC4 es un simple mejora de la ecuación de la FIB, logrado con mejor se ajuste de los exponentes y constantes. Para borrar el valor de la longitud, es necesario imponer condiciones a la búsqueda, que propone una primera función libre, no dependiente de la longitud, y un coeficiente de ajuste para el resto de parámetros: la ecuación PG_8v2R5 surge de esta manera. La marcada tendencia que exhibe el exponente (ls / db) al valor 0,5, induce un nuevo grupo de ejecuciones en las que se fije esta constante. Con este procedimiento, se obtiene la ecuación PG_7v3F2, lograr una distribución muy notable.

Some of the expressions stand out by different appearances. PG_9RSC4 is a simple improvement of the FIB equation, achieved with better adjusts of the exponents and constants. To clear the value of the length, it is necessary to impose conditions to the search, proposing a first free function, not dependent on the length, and a adjust coefficient for the rest of parameters: the equation PG_8v2R5 arises this way. The marked tendency that exhibits the exponent (ls/db) to the value 0.5, induces a new group of executions in which this constant is fixed. With this procedure, the PG_7v3F2 equation is obtained, achieving a very noticeable distribution.

En los últimos grupos notables, se permite la aparición de una función libre (sin ls) que multiplica ls con exponente constante y el término clásico de la contribución de refuerzo transversal, mejorado con constantes. Esta es la expresión PGcc6, que presentan una fuerte concentración alrededor de la unidad. A continuación, las tensiones que se pueden desarrollar para algunas variables específicas se comparan en dos de las ecuaciones que se encuentran frente a las expresiones FIB deducido. Se puede observar la similitud del enfoque, incluso para ecuaciones que no nacen de la estructura de la FIB.

Como resultado de lo expuesto anteriormente, se puede recomendar para adoptar la expresión PG_7v3F2 como una buena ecuación para obtener el comportamiento de bonos de la armadura pasiva en un elemento de hormigón.

In the last remarkable groups, it is allowed the apparition of a free function (without ls) that multiplies ls with constant exponent and the classical term of transversal reinforcement contribution, improved with constants. This is the PGcc6 expression, which exhibit a strong concentration around the unit. Next, the stresses that can be developed for some specific variables are compared in two of the equations found against the FIB deduced expressions. It can be observed the similarity of the approach, even for equations that are not born from the structure of the FIB.

As a result of the previously exposed, it can be recommended to adopt the expression PG_7v3F2 as a good equation to get the bond behavior of the passive reinforcement in a concrete element.

5 Conclusions

La ecuación FIB para determinar las barras de refuerzo tensión de tracción se mejoró con la aplicación de técnicas heurísticas.

En el método aplicado, seguridad estructural se tuvo en cuenta, a través de la ponderación contemplada por puntos fijos. Como conclusión final y resumen cabe señalar que se ha logrado implementar un nuevo método basado en la programación genética para extraer conocimiento a partir de datos experimentales basados en la experiencia. Esta experiencia se implementa a través de las limitaciones que son inducidos en el algoritmo.

FIB equation to determine rebar tension stress was improved with the application of heuristic techniques.

In the applied method, structural safety was taken into account, through the weighting provided by demerit points. As a final conclusion and summary it should be noted that it has managed to implement a novel method based on genetic programming to extract knowledge from experimental data based on the experience. This experience is implemented through constraints that are induced in the algorithm.

Acknowledgements.

 This work was partially supported by the Spanish Ministry of Science and Innovation (Ref. BIA2010-21551) and grants from the Ministry of Economy and Industry (Consellería de Economía e Industria) of the Xunta de Galicia (Ref. 10MDS014CT, Ref. 10TMT042E, Ref. 10TMT118004PR and Ref. 10TMT034E). 

References

1. Orangun, C.O., Jirsa, J.O., Breen, J.E.: A Reevaluation of Test Data on Development Length and Splices. ACI Journal 74(11), 114–122 (1977)

2. Tepfers, R.A.: Theory of bond applied to overlapped tensile reinforcement splices for deformed bars Ph.D. Thesis, Division of concrete structures, Chalmers University of Technology. Gothenburg, Sweden (1973)

3. Cairns, J.: Model for strength of lapped joints and anchorages. Paper presented at the meeting of the TG group 4.5 of the International Federation for Structural Concrete, Stuttgart, Germany (2006)

4. Abrams, D.A.: Tests of Bond Between Concrete and Steel. University of Illinois Bulletin Nº 71. University of Illinois, Urbana (1913)

5. FIB Task Group 4.5 “Bond models” (s.f) (2007), http://fibtg45.dii.unile.it/ (January 25, 2013)

6. Canbay, E., Frosch, R.: Bond strength of lap-spliced bars. ACI Structural Journal 102(4), 605–614 (2005)

7. Pérez, J.L., Cladera, A., Rabuñal, J.R., Martínez-Abella, F.: Optimization of existing equations using a new genetic programming algorithm: Application to the shear strength of reinforced concrete beams. Advances in Engineering Software 50(1), 82–96 (2012)

8. Ashour, A.F., Alvarez, L.F.: Toropov VV.: Empirical modeling of shear strength of RC deep beams by genetic programming. Computers & Structures 81(5), 331–338 (2003)

9. Pérez, J.L.: Metodología para orientar procesos de extracción de conocimiento basados en Computación Evolutiva. Aplicación al desarrollo de modelos y formulaciones en el ámbito del hormigón estructural, Ph.D. Thesis, Department of Information and Communication Technologies, University of A Coruña (2010).

10. Grandson, L.A. Taylor n-dimensional nets, The analytic equivalence to Neural Nets

Genetic Programming to Improvement FIB Model I / Programación Genética para el Mejoramiento del Modelo FIB I

Artículo patrocinado por Enmacosa dentro del proyecto "Formigón estructural", cofinanciado por la Xunta de Galicia (2013). 

Article sponsored by Enmacosa inside the "Formigón estructural" project, cofinanced by the Xunta de Galicia. (2013)

Adherencia y Anclaje de acero de refuerzo en Hormigón Estructural / Bond and Anchorage of Reinforcing Steel in Structural Concrete

Autores / Authors: Juan Luis Pérez (1), Ismael Vieito (2), Juan Rabuñal (3), and Fernando Martínez-Abella (2)

1 School of Building Engineering and Technical Architecture, University of A Coruña, Spain

2 Department of Construction Technology, University of A Coruña, Spain

3 Department of Information and Communication Technologies, University of A Coruña, Spain

Abstract.

Partiendo de la base de datos FIB, este trabajo está dirigido a analizar las ecuaciones actuales que predicen el dato principal que puede ser proporcionada por los ensayos previos: El ensayo de rotura de probetas de hormigón. Además, la programación genética (GP)  se aplica con el fin de mejorar la expresión de la FIB, que logra el mejor ajuste, hasta el momento, dando lugar al nuevo Código Modelo 2010. El resultado final que se muestra es una ecuación altamente predictiva. Los resultados se comparan con las incluidas en el Modelo y mostraron la influencia de las principales variables sobre el fenómeno (la resistencia del hormigón, límite elástico del acero, recubrimiento de hormigón, armadura transversal y el diámetro de la barra).

Starting from the FIB database, this work is aimed to analyze the current equations which predict the main datum that can be provided by bond tests: the ultimate bar stress when the failure is reached. Furthermore, Genetic Programming (GP) techniques are also applied in order to enhance the expression of the FIB, which achieves the best adjustment so far, giving rise to the new Model Code 2010. The final result shown is a highly predictive equation. The results are compared with those included in the Model Code and it is showed the influence of the main variables on the phenomenon (concrete strength, yield strength of steel, concrete cover, transverse reinforcement and diameter of the bar).

1 Introduction

Desde los albores del siglo 20, cuando se realizaron los ensayos de Abrams, el vínculo entre el hormigón y el acero dio lugar a numerosas publicaciones científicas, pruebas complejas de laboratorio y muchos enfoques de códigos estructurales. Hay muy pocas expresiones que son tan diferentes al comparar las diversas normas, como las destinadas a la predicción de la longitud de anclaje de las barras de refuerzo en el hormigón estructural. Dos líneas principales fueron creados a partir de los trabajos realizados por Orangun, Jirsa y Breen [1], precursores de la ecuación código ACI, y los estudios realizados por Tepfers [2], que inspiró a los lineamientos del modelo, que conduce a la Eurocódigo. Las pruebas llevadas a cabo en España también fueron de gran importancia, ya que dieron lugar a una formulación específica, extremadamente conservador para el refuerzo de gran diámetro.

Since the dawn of the 20th century, when Abrams’s tests were performed, the bond between concrete and steel led to numerous scientific papers, complex laboratory tests and many approaches of structural codes. There are very few expressions that are so different when comparing the various rules, such as those aimed at predicting the anchorage length of reinforcing bars in structural concrete. Two main lines were created starting from the works carried out by Orangun, Jirsa & Breen [1], precursors of the ACI code equation, and the studies performed by Tepfers [2], which inspired the guidelines of the Model Code, leading to the Eurocode. The tests carried out in Spain also were of great importance, as they gave rise to a specific formulation, extremely conservative for large-diameter reinforcement.

A pesar de la variedad de enfoques, las tres líneas tienen un nexo común: las propuestas se desarrollan a partir de la evidencia experimental. A partir de una expresión fundamental de la tensión de adherencia, dependiente de una variable principal, se incorporan como un factor multiplicativo el efecto de otras variables. Cuando se realiza una prueba de extracción, un estado de tensión radial se genera alrededor de la barra que puede causar daño al hormigón circundante. El daño puede ser mitigado por la colocación de la armadura transversal. La figura 1 muestra gráficamente el fenómeno de una barra de anclaje [3]

Despite the varied approaches, the three lines have a common nexus: the proposals are developed from the experimental evidence. From a basic expression of bond stress, dependent on a main variable are incorporated as a multiplicative factor the effect of other variables When a pull-out test is performed, a state of radial tension is generated around the bar that can cause damage to the surrounding concrete. The damage can be mitigated by the placement of transverse reinforcement, and having adequate cover bar. Figure 1 shows graphically the phenomenon of a bar anchorage [3]

Fig. 1. Fenómeno de un anclaje de barra.
Fig. 1. Phenomenon of a bar anchorage

2 Modelo FIB / FIB Model

El grupo de trabajo TG4.5 de la Fédération Internationale du Beton (FIB) [5] ha estado trabajando durante mucho tiempo en el análisis del anclaje y las características de la adherencia de las barras de acero de refuerzo. Basado en la obra de Canbay y Frosch [6], el grupo se ha propuesto dos ecuaciones: la versión de 2006 (1) y la versión actual empleada en la elaboración del Código Modelo 2010 (2), que proporciona la resistencia que puede ser alcanzado en una barra anclada. Esta ecuación depende de los parámetros observados hasta ahora y está protegido por un contraste con una base de datos experimental fuerte.

Las variables descritas en ambas fórmulas corresponden a las tensiones de adherencia (σsu), resistencia a la compresión en probeta cilíndrica (Fc), diámetro de la barra (db), la longitud de la barra anclada (ls), máximo y recubrimientos mínimos de la barra (cmin, cmax) y el recubrimiento de la armadura transversal (KTR).

The workgroup TG4.5 of the Fédération Internationale du Beton (FIB) [5] has been working for a long time in the analysis of the anchorage and the bond characteristics of reinforcement steel bars. Based in the works of Canbay and Frosch [6], the group has proposed two equations: the version 2006 (1) and the current versi
on employed in the development of the Model Code 2010 (2), that provides the work stress that can be reached on an anchored bar. This equation depends on the parameters seen until now and is protected by a contrast with a strong experimental database.

The variables described in both formulas correspond to the bond stresses (σsu), compressive strength in cylindrical specimen (fc), diameter of the bar (db), length of anchored bar (ls), maximum and minimum coatings of the bar (cmin, cmax) and the contribution of the transverse reinforcement (Ktr).

.

2.1 Dataset

La base de datos contiene actualmente datos (variables y resultados medidos o calculados) correspondientes a 813 ensayos. Para aplicar técnicas GP para el análisis, el rango de la base de datos es consistente y las frecuencias de cada uno de los datos deben ser analizados. Teniendo en cuenta los datos de histograma de frecuencias, los filtros que se aplican y se aceptan son los recomendados por el FIB [5]. Uno de los más importantes está relacionada con la σsu, la tensión alcanzada por la barra durante la prueba. Cualquier probeta limita su máximo fy, la resistencia, el valor máximo que puede tener la relación σsu / fy es de 1.05. En otras variables de sus valores relativos también son limitados, por ejemplo, los relacionados con la cubierta de hormigón. Por lo tanto, se aplican los filtros sobre cmin / Cmax y Cmin / db. La Tabla 1 muestra los parámetros utilizados para el filtrado y el filtro finalmente aplicada.

The database currently contains data (variables and results measured or calculated) corresponding to 813 trials. As will be applied GP techniques for analysis, so that the database range is consistent and frequencies of each of the data must be analyzed. Considering the frequency histogram data, several filters are applied and are accepted those recommended by the FIB [5]. One of the most important is related to the output data σsu, the stress reached by the bar during the test. Since any bar limits its maximum stress fy, the maximum value that can take the relationship σsu/fy is 1.05. In other variables their relative values are also limited, for example those related to the concrete cover. Thus, filters over cmin/cmax and cmin/db are applied. Table 1 shows the parameters used for filtering and the filter finally applied.

Table 1. Filters applied to the dataset

Después de aplicar el filtro, el BD se reduce a un total de 628 ensayos, de los cuales el 77,5% (487 ensayos), por selección aleatoria, se utilizan para la formación, dedicando el 22,5% restante (141 ensayos) para comprobar. La Tabla 2 muestra el rango final de los datos en cada uno de los subconjuntos establecidos (formación y verificación).

En las expresiones FIB BD filtrados producir resultados cuya precisión se presenta en las siguientes secciones.

After applying the filter, the BD is reduced to a total of 628 trials, of which 77.5% (487 trials), by random selection, are used for training, dedicating the remaining 22.5% (141 trials) to check. Table 2 shows the final range of the data in each of the subsets set (training and verification).

On the BD filtered FIB expressions produce results whose accuracy is presented in the following sections.

Table 2. Distribution of data in subsets defined over the BD filtered

3 Method

Continua en / Continue on: http://carreteras-laser-escaner.blogspot.com/2014/11/genetic-programming-to-improvement-fib_26.html

We go into Fermat´s function II / Adentrándonos en la función de Fermat II

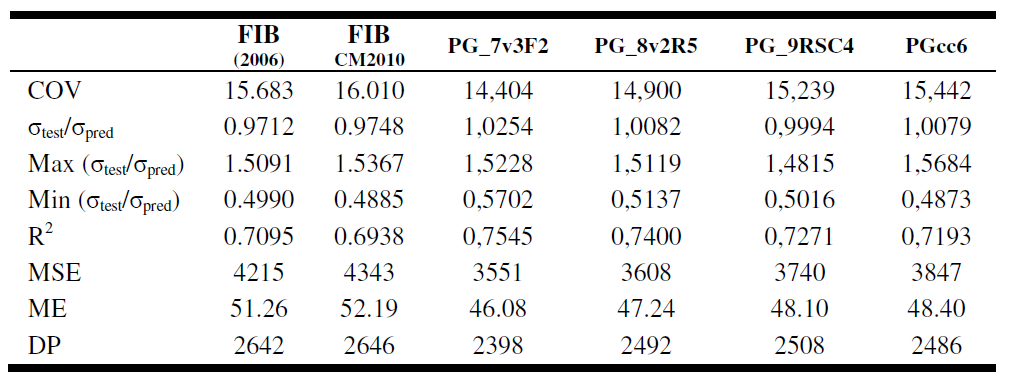
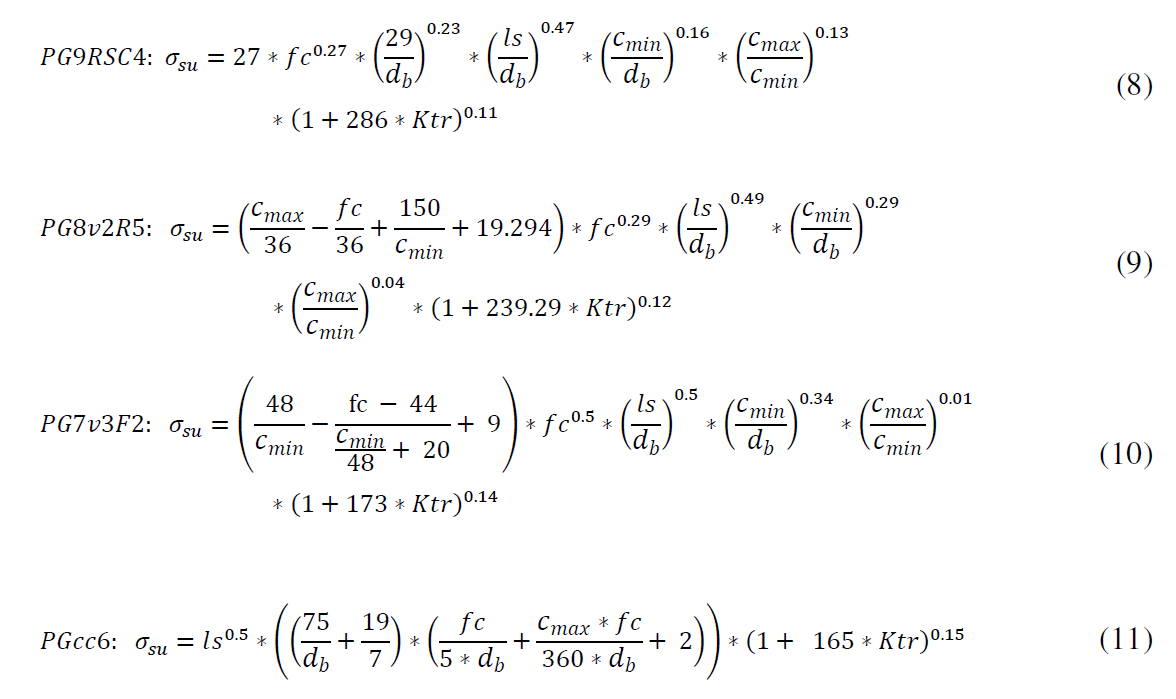Sea f, el valor que satisfaga / Let f, the value that satisfies:  a^f + b^f = c^f.

La direfencia con Fermat es que no obligaremos a que f sea un número natural. En su lugar buscaremos números f reales.
The difference with Fermat is that we will not force "f" was a natural number. Instead look real numbers for "f".

Conjuntos de tres / Sets of three elements

Lo primero es buscar el orden en las ternas {a, b, c}. La forma más fácil ser buscar los conjuntos que cumplan que la suma de sus elementos sean un número determinado y que c>a || b>a.

The first is to find order in the triples {a, b, c}. The easiest way to find the sets be satisfying than the sum of its elements are a certain number and c> a || b> a.

C(3) = {Ø}, 0 elementos.
C(4) = {( 1 1 2)} 1  elementos.
C(5) = {( 1 1 3), ( 1 2 2)} 2  elementos.
C(6) = {( 1 1 4), ( 1 2 3), ( 2 2 2)} 3  elementos.
C(7) = {( 1 1 5), ( 1 2 4), ( 1 3 3), ( 2 2 3)}
C(8) = {( 1 1 6), ( 1 2 5), ( 1 3 4), ( 2 2 4), ( 2 3 3)}
...
C(20) = {( 1 1 18), ( 1 2 17), ( 1 3 16), ( 1 4 15), ( 1 5 14), ( 1 6 13), ( 1 7 12), ( 1 8 11), ( 1 9 10), ( 2 2 16), ( 2 3 15), ( 2 4 14), ( 2 5 13), ( 2 6 12), ( 2 7 11), ( 2 8 10), ( 2 9 9), ( 3 3 14), ( 3 4 13), ( 3 5 12), ( 3 6 11), ( 3 7 10), ( 3 8 9), ( 4 4 12), ( 4 5 11), ( 4 6 10), ( 4 7 9), ( 4 8 8), ( 5 5 10), ( 5 6 9), ( 5 7 8), ( 6 6 8), ( 6 7 7)}  33 elementos.

Por si alguno tiene curiosidad el número de elementos de cada conjunto es:
In case anyone was curious, the number of elements in each set is:

( 2 0), ( 3 0), ( 4 1), ( 5 1), ( 6 2), ( 7 3), ( 8 4), ( 9 5), ( 10 7), ( 11 8), ( 12 10), ( 13 12), ( 14 14), ( 15 16), ( 16 19), ( 17 21), ( 18 24), ( 19 27), ( 20 30), ( 21 33), ( 22 37), ( 23 40), ( 24 44), ( 25 48), ( 26 52), ( 27 56), ( 28 61), ( 29 65), ( 30 70), ( 31 75), ( 32 80), ( 33 85), ( 34 91), ( 35 96), ( 36 102), ( 37 108), ( 38 114), ( 39 120), ( 40 127), ( 41 133), ( 42 140), ( 43 147), ( 44 154), ( 45 161), ( 46 169), ( 47 176), ( 48 184), ( 49 192), ( 50 200), ( 51 208), ( 52 217), ( 53 225), ( 54 234), ( 55 243), ( 56 252), ( 57 261), ( 58 271), ( 59 280), ( 60 290), ( 61 300), ( 62 310), ( 63 320), ( 64 331), ( 65 341), ( 66 352), ( 67 363), ( 68 374), ( 69 385), ( 70 397), ( 71 408), ( 72 420), ( 73 432), ( 74 444), ( 75 456), ( 76 469), ( 77 481), ( 78 494), ( 79 507), ( 80 520), ( 81 533), ( 82 547), ( 83 560), ( 84 574), ( 85 588), ( 86 602), ( 87 616), ( 88 631), ( 89 645), ( 90 660), ( 91 675), ( 92 690), ( 93 705), ( 94 721), ( 95 736), ( 96 752), ( 97 768), ( 98 784), ( 99 800), ( 100 817), ( 101 833),

Satisface la ecuación: y = 0,0833x2 - 0,1663x - 0,0207
Pero esto nos despista de nuestro objetivo

La idea / The idea

Una vez ordenados los conjuntos C(n) buscar los f de cada elemento del conjunto y ver que pinta tienen.Para cumplir este objetivo lo primero que hay que hacer es programar una función para calcular f conociendo a, b y c.

Once ordered sets C (n), we have to find the f of each element of the set and see how they are. To meet this objective the first thing to do is to make an function to calculate b and c knowing f.


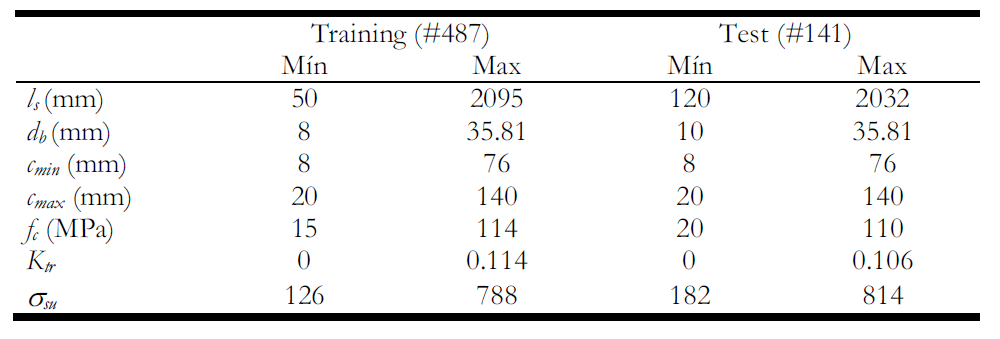
Function CalculaFa(ByVal a As Integer, 
                   ByVal b As Integer,
                   ByVal c As Integer) As Double
g = 0:p = 0.1:i1 = Sgn(a ^ g + b ^ g - c ^ g)
100:
Do
  i0 = i1: g = g + p
  h1 = a ^ g + b ^ g - c ^ g
  i1 = Sgn(h1)
Loop Until i0 <> i1
p = -p / 10
If Abs(p) > 0.0000001 Then GoTo 100
CalculaFa = g
End Function



Resultado numérico: / Numerical results:

C(5): (1 1 3)→0,630930 (1 2 2)→Inf.  C(6): (1 1 4)→0,500000 (1 2 3)→1,000000 (2 2 2)→Inf.  C(7): (1 1 5)→0,430677 (1 2 4)→0,694242 (1 3 3)→Inf. (2 2 3)→1,709511  C(8): (1 1 6)→0,386853 (1 2 5)→0,563896 (1 3 4)→1,000000 (2 2 4)→1,000000 (2 3 3)→Inf. C(9): (1 1 7)→0,356207 (1 2 6)→0,489536 (1 3 5)→0,727160 (1 4 4)→Inf. (2 2 5)→0,756471 (2 3 4)→1,507127 (3 3 3)→Inf.  C(10): (1 1 8)→0,333333 (1 2 7)→0,440660 (1 3 6)→0,600967 (1 4 5)→1,000000 (2 2 6)→0,630930 (2 3 5)→1,000000 (2 4 4)→Inf. (3 3 4)→2,409421  C(11): (1 1 9)→0,315465 (1 2 8)→0,405685 (1 3 7)→0,525764 (1 4 6)→0,748222 (1 5 5)→Inf. (2 2 7)→0,553295 (2 3 6)→0,787885 (2 4 5)→1,421586 (3 3 5)→1,356916 (3 4 4)→Inf.

C(12): (1 1 10)→0,301030 (1 2 9)→0,379195 (1 3 8)→0,474995 (1 4 7)→0,626250 (1 5 6)→1,000000 (2 2 8)→0,500000 (2 3 7)→0,668850 (2 4 6)→1,000000 (2 5 5)→Inf. (3 3 6)→1,000000 (3 4 5)→2,000000 (4 4 4)→Inf.  C(13): (1 1 11)→0,289065 (1 2 10)→0,358299 (1 3 9)→0,438018 (1 4 8)→0,551463 (1 5 7)→0,763203 (1 6 6)→Inf. (2 2 9)→0,460846 (2 3 8)→0,591710 (2 4 7)→0,807572 (2 5 6)→1,372508 (3 3 7)→0,818068 (3 4 6)→1,293174 (3 5 5)→Inf. (4 4 5)→3,106284  C(14): (1 1 12)→0,278943 (1 2 11)→0,341305 (1 3 10)→0,409664 (1 4 9)→0,500000 (1 5 8)→0,645009 (1 6 7)→1,000000 (2 2 10)→0,430677 (2 3 9)→0,537187 (2 4 8)→0,694242 (2 5 7)→1,000000 (2 6 6)→Inf. (3 3 8)→0,706695 (3 4 7)→1,000000 (3 5 6)→1,822550 (4 4 6)→1,709511 (4 5 5)→Inf.

C(15): (1 1 13)→0,270238 (1 2 12)→0,327153 (1 3 11)→0,387098 (1 4 10)→0,462006 (1 5 9)→0,571072 (1 6 8)→0,774576 (1 7 7)→Inf. (2 2 11)→0,406598 (2 3 10)→0,496338 (2 4 9)→0,618529 (2 5 8)→0,821352 (2 6 7)→1,339977 (3 3 9)→0,630930 (3 4 8)→0,836778 (3 5 7)→1,256656 (3 6 6)→Inf. (4 4 7)→1,238613 (4 5 6)→2,487939 (5 5 5)→Inf.  C(16): (1 1 14)→0,262650 (1 2 13)→0,315140 (1 3 12)→0,368624 (1 4 11)→0,432581 (1 5 10)→0,519463 (1 6 9)→0,659684 (1 7 8)→1,000000 (2 2 12)→0,386853 (2 3 11)→0,464425 (2 4 10)→0,563896 (2 5 9)→0,712809 (2 6 8)→1,000000 (2 7 7)→Inf. (3 3 10)→0,575717 (3 4 9)→0,731774 (3 5 8)→1,000000 (3 6 7)→1,719845 (4 4 8)→1,000000 (4 5 7)→1,581624 (4 6 6)→Inf. (5 5 6)→3,801784

C(17): (1 1 15)→0,255958 (1 2 14)→0,304786 (1 3 13)→0,353161 (1 4 12)→0,408985 (1 5 11)→0,480955 (1 6 10)→0,586741 (1 7 9)→0,783603 (1 8 8)→Inf. (2 2 13)→0,370310 (2 3 12)→0,438694 (2 4 11)→0,522352 (2 5 10)→0,638731 (2 6 9)→0,831677 (2 7 8)→1,316498 (3 3 11)→0,533484 (3 4 10)→0,658051 (3 5 9)→0,849761 (3 6 8)→1,232521 (3 7 7)→Inf. (4 4 9)→0,854756 (4 5 8)→1,207399 (4 6 7)→2,215951 (5 5 7)→2,060043 (5 6 6)→Inf.  C(18): (1 1 16)→0,250000 (1 2 15)→0,295743 (1 3 14)→0,339986 (1 4 13)→0,389554 (1 5 12)→0,450889 (1 6 11)→0,535259 (1 7 10)→0,671597 (1 8 9)→1,000000 (2 2 14)→0,356207 (2 3 13)→0,417433 (2 4 12)→0,489536 (2 5 11)→0,584449 (2 6 10)→0,727160 (2 7 9)→1,000000 (2 8 8)→Inf. (3 3 12)→0,500000 (3 4 11)→0,603151 (3 5 10)→0,749960 (3 6 9)→1,000000 (3 7 8)→1,651588 (4 4 10)→0,756471 (4 5 9)→1,000000 (4 6 8)→1,507127 (4 7 7)→Inf. (5 5 8)→1,474770 (5 6 7)→2,973549 (6 6 6)→Inf.

C(19) (1 1 17)→0,244651 (1 2 16)→0,287761 (1 3 15)→0,328594 (1 4 14)→0,373214 (1 5 13)→0,426624 (1 6 12)→0,496517 (1 7 11)→0,599669 (1 8 10)→0,791002 (1 9 9)→Inf. (2 2 15)→0,344010 (2 3 14)→0,399514 (2 4 13)→0,462854 (2 5 12)→0,542693 (2 6 11)→0,654699 (2 7 10)→0,839780 (2 8 9)→1,298569 (3 3 13)→0,472707 (3 4 12)→0,560499 (3 5 11)→0,678323 (3 6 10)→0,859418 (3 7 9)→1,215158 (3 8 8)→Inf. (4 4 11)→0,685198 (4 5 10)→0,867160 (4 6 9)→1,186814 (4 7 8)→2,057504 (5 5 9)→1,179250 (5 6 8)→1,867720 (5 7 7)→Inf. (6 6 7)→4,496556

C(20): (1 1 18)→0,239813 (1 2 17)→0,280648 (1 3 16)→0,318622 (1 4 15)→0,359240 (1 5 14)→0,406541 (1 6 13)→0,466065 (1 7 12)→0,548456 (1 8 11)→0,681533 (1 9 10)→1,000000 (2 2 16)→0,333333 (2 3 15)→0,384168 (2 4 14)→0,440660 (2 5 13)→0,509415 (2 6 12)→0,600967 (2 7 11)→0,738690 (2 8 10)→1,000000 (2 9 9)→Inf. (3 3 14)→0,449966 (3 4 13)→0,526285 (3 5 12)→0,624114 (3 6 11)→0,763919 (3 7 10)→1,000000 (3 8 9)→1,602326 (4 4 12)→0,630930 (4 5 11)→0,774279 (4 6 10)→1,000000 (4 7 9)→1,457470 (4 8 8)→Inf. (5 5 10)→1,000000 (5 6 9)→1,412357 (5 7 8)→2,605651 (6 6 8)→2,409421 (6 7 7)→Inf. ...

C(25): (1 1 23)→0,221065 (1 2 22)→0,253971 (1 3 21)→0,282600 (1 4 20)→0,311047 (1 5 19)→0,341358 (1 6 18)→0,375361 (1 7 17)→0,415359 (1 8 16)→0,464959 (1 9 15)→0,530840 (1 10 14)→0,628226 (1 11 13)→0,807162 (1 12 12)→Inf. (2 2 21)→0,294784 (2 3 20)→0,331166 (2 4 19)→0,368173 (2 5 18)→0,408588 (2 6 17)→0,455182 (2 7 16)→0,511801 (2 8 15)→0,584974 (2 9 14)→0,688046 (2 10 13)→0,856493 (2 11 12)→1,262874 (3 3 19)→0,375521 (3 4 18)→0,421736 (3 5 17)→0,473532 (3 6 16)→0,535062 (3 7 15)→0,612636 (3 8 14)→0,717976 (3 9 13)→0,878073 (3 10 12)→1,182930 (3 11 11)→Inf. (4 4 17)→0,479051 (4 5 16)→0,545214 (4 6 15)→0,626613 (4 7 14)→0,733936 (4 8 13)→0,889217 (4 9 12)→1,151962 (4 10 11)→1,817457 (5 5 15)→0,630930 (5 6 14)→0,741031 (5 7 13)→0,894776 (5 8 12)→1,137374 (5 9 11)→1,623440 (5 10 10)→Inf. (6 6 13)→0,896477 (6 7 12)→1,131270 (6 8 11)→1,552882 (6 9 10)→2,720194 (7 7 11)→1,533562 (7 8 10)→2,436346 (7 9 9)→Inf. (8 8 9)→5,884949

Resultado gráfico: / Graphic results:


Cada banda vertical es un número f, azul para C(1) y rojo para C(255) según arco iris
Each vertical strip is a number f, blue for C (1) and red for C (255) according rainbow scale.

Ídem, pero en lugar de formar una banda vertical, forma un punto y en ordenadas el valor de x de C(x).
Idem, but instead of forming a vertical band, it forms a neat point and the value of x in C (x).

Salvo ante valores de 0, 1 y 2 parece que los némeros "f" rehuyeran los demás números enteros, y quebrados y similares. Se puede concluir que: "x Î R, $ fÎ[x-e,x+e]Î R & a,b,c Î N | a^f+b^f=c^f . Es decir, dado un número real, x, siempre existe un número real en el intervalo [x-e,x+e] que satisface la ecuación a^f+b^f=c^f con valores enteros de a,b y c.

Pongamos un ejemplo. Sea x=3, vamos a ver cómo podemos aproximarnos:

 C(10); (3 3 4);       f = 2,409421;  e = 0,590579

 C(13); (4 4 5);       f = 3,106284;  e = 0,106283

 C(18); (5 6 7);       f = 2,973549;  e = 2,645111·10^-02

 C(23); (6 8 9);       f = 2,993245;  e = 6,755113·10^-03

 C(31); (9 10 12);     f = 3,002552;  e = 2,552032·10^-03

 C(82); (15 33 34);    f = 3,002088;  e = 2,088069·10^-03

 C(98); (17 40 41);    f = 2,998646;  e = 1,353979·10^-03

C(113); (23 44 46);    f = 3,001228;  e = 1,228094·10^-03

C(119); (36 37 46);    f = 2,998798;  e = 1,202106·10^-03

C(120); (24 47 49);    f = 2,999859;  e = 1,409053·10^-04

C(166); (43 58 65);    f = 2,999891;  e = 1,089572·10^-04

C(216); (41 86 89);    f = 3,000106;  e = 1,060962·10^-04

C(261); (64 94 103);   f = 3,000005;  e = 5,006790·10^-06

C(353); (71 138 144);  f = 2,999997;  e = 3,099441·10^-06

C(445); (135 138 172); f = 2,999999;  e = 9,536743·10^-06

La sucesión 10, 23, 28, 23, 31, 82, 98, 113, 119, 120, 166
, 216, 261, 353, 445,... ¿Tiene algún término general?

Para x=4

 C(13); (4 4 5);      f = 3,106284;  e = 0,8937160
 C(16); (5 5 6);      f = 3,801784;  e = 0,1982159
 C(24); (7 8 9);      f = 3,941391;  e = 5,860900·10^-02
 C(37); (10 13 14);   f = 4,026536;  e = 2,653598·10^-02
 C(59); (18 19 22);   f = 4,025973;  e = 2,597284·10^-02
 C(67); (16 25 26);   f = 3,982761;  e = 1,723909·10^-02
 C(72); (17 27 28);   f = 4,005021;  e = 5,021095·10^-03
 C(94); (21 36 37);   f = 3,999590;  e = 4,100799·10^-04
C(118); (37 37 44);   f = 4,000348;  e = 3,480911·10^-04
C(184); (53 62 69);   f = 3,999917;  e = 8,296966·10^-05
C(320); (64 127 129); f = 3,999935;  e = 6,508827·10^-05

Con e = 0,01 resulta:

C(23); (6 8 9); f = 2,993245
C(31); (9 10 12); f = 3,002552
C(46); (12 16 18); f = 2,993245
C(62); (18 20 24); f = 3,002552
C(69); (18 24 27); f = 2,993245
C(74); (19 26 29); f = 3,009558
C(75); (23 23 29); f = 2,990260
C(80); (23 26 31); f = 2,992867
C(82); (15 33 34); f = 3,002088
C(88); (27 27 34); f = 3,006838
C(91); (22 33 36); f = 2,991530
C(92); (24 32 36); f = 2,993245
[...]
C(171); (44 60 67); f = 3,007065

C(173); (50 56 67); f = 2,997841
[...]

Con e = 0,001 resulta:

C(120); (24 47 49); f = 2,999859
C(146); (31 56 59); f = 3,000988
C(163); (50 50 63); f = 2,999187
C(166); (43 58 65); f = 2,999891
C(179); (26 76 77); f = 3,000766
C(186); (40 71 75); f = 3,000602
[...]
C(319); (88 107 124); f = 2,999737

[...]

Con e = 0,0001 resulta:

C(261); (64  94 103); f = 3,000005
C(318); (94 101 123); f = 3,000042
C(328); (95 106 127); f = 3,000017
C(349);(103 111 135); f = 2,999970
C(353); (71 138 144); f = 2,999997
C(367); (73 144 150); f = 3,000003
C(374); (83 141 150); f = 3,000016
C(378); (54 161 163); f = 2,999991
C(380);(112 121 147); f = 2,999953
C(381); (44 168 169); f = 3,000049
C(400);(107 137 156); f = 2,999975
C(409);(102 146 161); f = 3,000080
C(411);(121 131 159); f = 2,999971
C(429); (59 184 186); f = 3,000089
C(432);(130 135 167); f = 2,999918
C(442);(130 141 171); f = 3,000009
C(445);(135 138 172); f = 2,999999

C(451);(120 155 176); f = 3,000087

[...]

De todo esto se puede deducir que si bien el teorema de Fermat se cumple para un matemático, sin embargo, se incumple para un ingeniero (si se admite un pequeño error). :-)

From all this, it can be deduced that although Fermat's theorem is true for a mathematician, however, fails to engineer (if a little error is supported). :-)

Queda ver que pasa cuando f forme parte de los números complejos.
It remains to see what happens when f was part of the complex numbers.