Artículo patrocinado por Enmacosa dentro del proyecto "Formigón estructural", cofinanciado por la Xunta de Galicia (2013).
Continía de: http://carreteras-laser-escaner.blogspot.com/2014/11/regresion-simbolica-en-ingenieria-civil.html
A. Comparación con la PG clásica
En la Tabla 3 se muestra la configuración empleada para el conjunto de pruebas realizadas. El ajuste se ha realizado mediante el error cuadrático medio combinado con el valor de parsimonia. El criterio de terminación que se ha adoptado para el conjunto de pruebas ha sido que, o bien se alcanza la generación máxima, (establecido en 10.000 generaciones) o bien se alcanza un ECM ≈0.
 |
| TABLA II. RANGO DE LOS DATOS DE LOS COMPONENTES |
 |
| TABLA III. PARÁMETROS DEL PROBLEMA |
 |
| TABLA IV. PARÁMETROS PROPIOS DE DISTCLUSTPG |
Como se puede observar en la Tabla 3, se ha elegido un valor atípico de probabilidad de mutación. Tras realizar un conjunto de pruebas con distintos valores de dicha probabilidad (0.1%, 0.5%, 1%, 2% y 5%) y permitiendo una gran altura de los árboles, el valor elegido ha sido el del 5% por ser el que mejores resultados ha proporcionado.
La función de fitness utilizada en este problema ha sido el error cuadrático medio (ECM), cuya fórmula puede verse en la ecuación (6).
donde ek es el error cometido para el patrón k. Se realizaron un conjunto de pruebas mediante la PG clásica y otra mediante el sistema desarrollado. Con el objetivo de que ambos métodos puedan ser comparables, se ha empleado la misma configuración de parámetros y se han realizado las pruebas en los mismos equipos (Intel® Core™ 2 Duo E6550 2.33GHz 1GB RAM). Los parámetros propios del sistema desarrollado se muestran en la Tabla 4.
El resultado del conjunto de pruebas con la PG clásica puede verse en la Figura 3. Para facilitar la comparación de los resultados, de las 50 ejecuciones de PG clásica, se han elegido las 6 ejecuciones con valores centrales (puesto que el sistema desarrollado ha empleado un total de 6 nodos), y se ha calculado su media. Los valores de ajuste obtenidos tras 5000 generaciones han sido los mostrados en la Tabla 5.
A continuación se detalla la prueba del sistema desarrollado con 6 nodos para el problema de resistencia del hormigón, estableciendo la periodicidad del algoritmo de Clustering a 100
generaciones. |
| TABLA V. VALORES DE AJUSTE OBTENIDOS CON PG CLÁSICA |
Como se puede observar en la Figura 4, el sistema desarrollado supera el valor medio de ajuste obtenido con PG clásica, pues en la generación 5.000 todos los nodos han alcanzado el valor de ajuste 50.3618.
Para comprobar la coevolución de los nodos, la Figura 5 muestra la evolución de los distintos nodos esclavo junto al maestro. En la figura se puede observar que cuando uno de los nodos alcanza un valor óptimo, gracias al proceso de migración de los mejores individuos de cada clúster, ayuda a los demás a alcanzar rápidamente ese valor. Gracias a que cada nodo conserva individuos de poblaciones originales independientes, el sistema puede seguir explorando diferentes espacios de búsqueda.
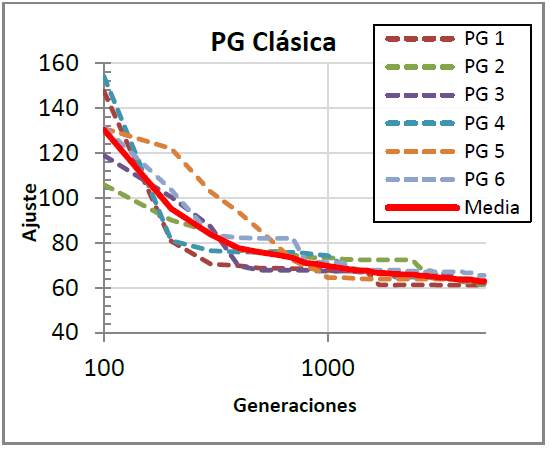 |
| Fig. 3. Media de las ejecuciones de PG clásica |
 |
| Fig. 4. Evolución del fitness en DistClustPG |
 |
| Fig. 5. Coevolución de los nodos |
B. Comparación con otros métodos
A continuación se comparan los resultados del sistema distribuido con otros trabajos previos en los cuales se utilizaron Redes de Neuronas Artificiales [14], [15]. En la Tabla 6, se muestran los resultados obtenidos en [14] en forma de coeficiente de determinación.
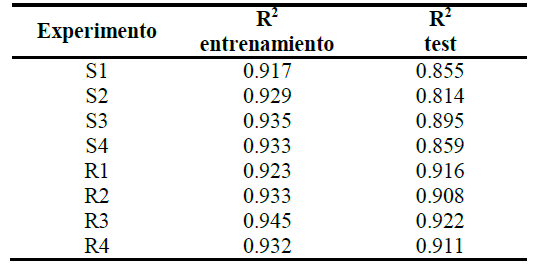 |
| TABLA VI. RESULTADOS DE LA RED NEURONAL |
En [15], se obtiene un R2 con el conjunto de test de 0.919. En la Tabla 7 se muestran los errores obtenidos con el sistema distribuido (error medio, error cuadrático medio y covarianza). Con el sistema distribuido se ha obtenido un R2 en entrenamiento de 0.8182 y del 0.774 con el conjunto de test.
 |
| TABLA VII. ERRORES OBTENIDOS CON DISTCLUSTPG |
En la siguiente tabla se muestran los valores de R^2 de las distintas aproximaciones.
 | ||
| TABLA VIII. COMPARACIÓN R^2 | EN TEST |
Normalmente, los resultados obtenidos mediante las redes de neuronas artificiales son mejores si los comparamos directamente con la aplicación de la programación genética. Pero con una gran salvedad, con las redes se obtiene una caja negra con la que únicamente se relacionan variables de entrada con la salida, en
cambio con la PG se obtiene una expresión que hace explícitas las relaciones con las variables que intervienen en el problema. Es esta la razón por la cual se hace útil en el ámbito de la Ingeniería Civil.
Además de los métodos anteriores, se han realizado experimentos con Algoritmos Genéticos utilizando la aplicación GeneXproTools 4.05. En la Tabla 9 se muestran los resultados de 6 de las pruebas realizadas, para que dichos resultados sean comparables a los métodos anteriores. Los parámetros utilizados han sido los mismos que los utilizados para los otros sistemas.
 |
| TABLA IX . RESULTADOS DE GENEXPROTOOLS |
Como se puede observar en la tabla anterior, y si comparamos con la Tabla 7 donde aparecían los resultados de DistClustPG, el método de algoritmos genéticos obtiene peores resultados tanto en términos de ECM como de R2. En el mejor de los casos, la fórmula obtenida ha
sido la siguiente:
donde di son las variables de entrada. Sin embargo, por término medio, las soluciones de GeneXproTools tienen un tamaño de 25 nodos. Tras la ejecución de DistClustPG se consigue modelar el comportamiento de la resistencia del hormigón materializado en la fórmula 8.
Para el caso de sp=0 la ecuación resultante es más sencilla que la obtenida con el método anterior. Aunque para el caso sp≠0 la solución tenga un mayor número de nodos que la media de GeneXproTools, gracias al proceso de clustering en función de la diferencia estructural de los árboles se han obtenido varias soluciones
que aun siendo algo peores en términos de fitness, son más sencillas (constan por término medio de 17 nodos) y por lo tanto, resultan más útiles a los Ingenieros Civiles.
IV. CONCLUSIONES
Una de las principales aportaciones de este trabajo es que se trata de una implementación eficiente de un sistema de PG paralelo de fácil manejo para el experto en Ingeniería Civil. Además, la evaluación del sistema ha demostrado que las soluciones proporcionadas mejoran en relación con las obtenidas mediante PG clásica.
Otro factor a tener en cuenta es que las poblaciones son más heterogéneas durante su evolución, disminuyendo el riesgo de caer en mínimos locales o facilitando un salto a otras zonas del espacio de búsqueda gracias a la migración de individuos.
Los expertos disponen con este sistema de otra medida distinta del valor de fitness para tomar sus decisiones y que les facilite la ardua tarea de interpretación de los resultados. Esta medida es la complejidad estructural de las fórmulas.
Gracias a la distribución del trabajo, el número de pruebas necesarias para la obtención de un resultado satisfactorio disminuye considerablemente, reduciendo a su vez el coste humano y de recursos asociado.
Por último, el uso de técnicas de Programación Genética frente a otras aproximaciones como las redes neuronales, permite que las relaciones entre las variables del problema sean explícitas, aportando como solución formulaciones matemáticas de más fácil comprensión y aplicación para el experto en Ingeniería Civil.
AGRADECIMIENTOS
Este trabajo ha sido cofinanciado por el Ministerio de Ciencia e Innovación (Ref. BIA2010-21551 y Ref. TIN2009-07707), y por la Consellería de Economía e Industria perteneciente a la Xunta de Galicia (Ref.10SIN105004PR, Ref. 10MDS014CT y Ref. 10TMT034E).
REFERENCIAS
[1] Koza J R (1992) Genetic Programming: On the Programming of Computers by Means of Natural Selection. Cambridge, MA: MIT Press.
[2] Catoira A, Pérez J L, Rabuñal J R (2010). Distributed Genetic Programming for obtaining formulas: application to concrete strength. DCAI 2010. Valencia. Spain.
[3] Dubes R C and Jain A K (1988) Algorithms for Clustering Data. Cambridge, MA: MIT Press.
[4] Gan G, Ma C and Wu J (1979) Data Clustering: Theory, Algorithms and Applications. ASASIAM, Pennsylvania.
[5] ANL Mathematics and Computer Science (2010) MPI: A Message Passing Interface Standard. http://www.mcs.anl.gov/research/projects/mpi/
[6] Gran G., Man C., Wu J. (1979). Data Clustering: Theory, Algorithms and Applications. ASA-SIAM, Pennsylvania.
[7] Dubes R. C., Jain A. K. (1988). Algorithms for Clustering Data. Cambridge, MA: MIT Press.
[8] Ékart A., Németh S. Z. (2002). Maintaining the diversity of genetic programs, Lecture Notes in Computer Science (EUROGP 2002). No. 2278. pp 162-171.
[9] Chang T P, Chung C, Ling H C. Inst. Eng, 19, 645.
[10] Domone P L J, Soutsos M N. Concr. Int, 26.
[11] Abrams DA. (1918) Desing of Concrete Mixtures. Bulletin nº1, Structural Materials Research Laboratory, Lewis Institute, Chicago.
[12] Oluokun F A. ACI Mater, 91, 362.
[13] Popovics S. ACI Mater, 87, 517.
[14] Yeh I-C. Modeling of strength of highperformance concrete using artificial neural networks (1998). Cement and Concrete Research. Vol 28, No. 12, pp. 1797-1808.
[15] Yeh I-C. A Mix Proportioning for fly ash and slag concrete using artificial neural networks (2003). Chung Hua Journal of Science and Engineering. Vol. 1, No. 1, pp. 77-84. [16] UCI Machine Learning Repository.
[16] Grandson, L.A. Taylor n-dimensional nets, The analytic equivalence to Neural Nets
[16] Grandson, L.A. Taylor n-dimensional nets, The analytic equivalence to Neural Nets
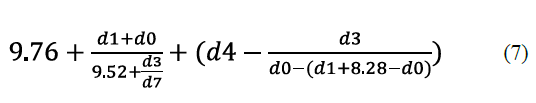
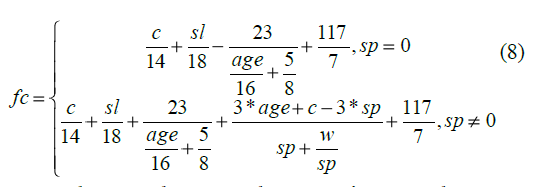
No hay comentarios:
Publicar un comentario