Artículo patrocinado por Enmacosa dentro del proyecto "Formigón estructural", cofinanciado por la Xunta de Galicia (2013).
Continúa de: http://carreteras-laser-escaner.blogspot.com/2014/12/mejora-de-la-formulacion-del-ec-2-para.html
4 Resultados
Tras la aplicación del método, más de 1000 veces, se han conseguido un conjunto de expresiones, de distinta complejidad. En este caso se han seleccionado 3 fórmulas que combinan perfectamente la sencillez y capacidad de predicción. La denominada 11G1-GP1 (5) basada en la ecuación (3) y cumpliendo las restricciones impuestas (Tabla 3, restricción G). De igual manera se han seleccionado las ecuaciones 12H1-GP4 (6) y 12I1(7), que surgen de la ecuación (4) cumpliendo las restricciones H e I respectivamente.
En la Tabla 5 se muestra el ajuste comparado mostrado por las formulaciones normativas actuales (EC-2, ACI11-3 y ACI11-5) y las ecuaciones propuestas en este artículo (11G1-GP1 (5), 11H1-GP4 (6), 12I1(7)) frente a la base de datos utilizada. En ella se presentan el valor del coeficiente de variación COV, la ratio Vens/Vpred (promedio del cociente del valor obtenido en el ensayo entre el valor calculado mediante los distintos modelos), R2 (cuadrado del coeficiente de correlación de momento del producto Pearson), los errores cuadrático medio (ECM) y medio (EM) y los puntos de demérito (PD). En [10] se pueden consultar las fórmulas utilizadas para el cálculo. Como puede verse en dicha tabla las ecuaciones desarrolladas por el algoritmo propuesto mejoran la correlación del EC-2 y de las formulaciones del código ACI318-05 (ecuaciones 11-3 y 11-5 de dicha normativa).
 |
| Tabla 5. Resultados entrenamiento y test. |
Se puede obtener más información sobre las correlaciones de las fórmulas 11G1 y 12H1 en la referencia [9], bajo la denominación GP-1 y GP-4 respectivamente. Estas ecuaciones fueron inicialmente seleccionadas, por su gran sencillez de uso, si bien la ecuación 12I1 debe también ser tenida en cuenta.
Cabe destacar el aumento de seguridad conseguido, visible gráficamente en la Figura 4, que muestra la correlación del EC-2 y la ecuación 12I1. La zona sombreada corresponde a valores inseguros de las predicciones.
 |
| Figura 4. Correlación entre valor de ensayo y valor de predicción |
5 Interacción momento flector – esfuerzo cortante
Las ecuaciones propuestas 12H1-GP4 y 12I1 introducen el término V·d/M o V/M, considerando por tanto la influencia de la relación entre el momento flector concomitante y el esfuerzo cortante.
En la Figura 5 se presenta el diagrama de interacción momento último-cortante obtenido según el EC-2, las ecuaciones propuestas 12H1 y 12I1, la ecuación 11G1 y mediante el programa Response 2000 [11], basado en la Teoría Modificada del Campo de Compresiones [6].
 |
| Figura 5. Diagrama de interacción momento flector – cortante en función del canto de la viga (bw = 250 mm, fc = 25 MPa, ρl = 0.689%) |
Los valores adimensionales representados en la Figura 5 se obtienen de la ecuación (8):
Para la representación gráfica de los resultados de las ecuaciones 12H1-GP4 y 12I1 se han utilizado, en este apartado, los valores límites dados por la ecuación (9). Estos límites no son de aplicación para ninguna de las vigas de la base de datos, pero es necesario establecerlos para extender el uso de las ecuaciones a vigas cortas con un valor pequeño del cociente a/d.
Se observa que el EC-2 no presenta interacción momento-cortante hasta valores elevados del momento flector. Por el contrario, las sencillas ecuaciones 12H1 y 12I1 predicen la interacción para cualquier valor del momento flector concomitante, con un comportamiento muy similar al dado por el modelo sofisticado de la Teoría Modificada del Campo de Compresiones (Response-2000). Los valores dados por la ecuación 11G1-GP1 son aproximadamente los valores medios predichos por Response-2000, siendo algo conservadores para momentos adimensionales bajos y algo inseguros para altos valores del momento flector adimensional. El efecto del incremento del canto de la viga puede verse claramente en la Figura 6 para las distintas formulaciones. El procedimiento dado por el EC-2 es, comparado con los resultados del Response-2000, inseguro para momentos concomitantes elevados. Este efecto es especialmente notable para vigas de gran canto. En la Figura 6 no se representa la gráfica para la ecuación 12I1 puesto que sería muy similar a la dada para 12H1-GP4.
Tener en cuenta la interacción momento-cortante tiene efectos en la influencia de la cuantía de armadura longitudinal. La Figura 7 resume dicha influencia según los diferentes métodos de cálculo a cortante. En la Figura 7a se muestra la evolución de la tensión a cortante al incrementar el valor de la cuantía longitudinal, rol
, manteniendo constantes los restantes parámetros. En este caso, las ecuaciones representadas (EC-2, 11G1-GP1, 12H1-GP4, 12I1) muestran un comportamiento similar para bajas cuantías de armado longitudinal. Para valores superiores al 2%, el EC-2 no considera mayores incrementos en la tensión última a cortante, mientras que la tensión sigue aumentado para las formulaciones propuestas con las técnicas de PG.
 |
| Figura 6. Diagramas de interacción momento-cortante en función del canto de la viga. |
En la Figura 7b se ha aumentado la luz a cortante a medida que se aumenta la cuantía de armadura longitudinal, consiguiendo mantener constante la tensión de tracción en la armadura o, lo que es equivalente, se mantiene constante el valor del parámetro M/ρl·V·d. Se observa que las predicciones del EC-2 y de 11G1-GP1 son idénticas que en el caso anterior (Figura 7a). Sin embargo, para las formulaciones 12H1-GP4 y 12I1, la tensión última a cortante crece en mucha menor medida que cuando únicamente se aumentaba la cuantía de armadura longitudinal.
 |
| Figura 7. Influencia de la cuantía de armadura longitudinal. a) Vigas con a/d constante. b) Vigas con M/ρl·V·d constante. |
6 Conclusiones
El algoritmo empleado es un método válido para el ajuste de expresiones ya existentes, permitiendo elegir en qué términos es susceptible de ser mejorada definiendo para este cometido un conjunto de restricciones. Las restricciones pueden referirse tanto a la elección de las variables a emplear (dentro del conjunto de datos), como al tipo de operadores (terminales y no terminales) permitidos en la generación de nuevos individuos.
Con el conjunto de pruebas realizadas se demuestra la capacidad del algoritmo empleado, obteniéndose unos resultados mejores que las normativas internacionales analizadas. La potencia del método se destaca al alcanzar fórmulas de gran sencillez, como las 3 ecuaciones presentadas (11G1-GP1, 12H1-GP4 y 12I1), que podrían ser tenidas en cuenta para incorporarlas a la normativa como modelo de predicción de la resistencia a cortante en vigas de hormigón sin armadura de cortante. En especial, la ecuación 12I1 ofrece, además de sencillez, unos muy buenos resultados.
En la obtención de los resultados finales ha sido fundamental el refinamiento de las restricciones, siendo una labor iterativa que ha involucrado a Ingenieros Civiles y a Ingenieros Informáticos, trabajando en equipo.
7 Agradecimientos
Este trabajo ha sido cofinanciado por el Ministerio de Ciencia e Innovación (BIA2007-60197 y BIA2010-21551), y por la Consellería de Economía e Industria perteneciente a la Xunta de Galicia (Ref. 08TMT005CT y Ref. 10TMT034E).
8 Bibliografía
[1] EC-2. Design of concrete structures Part I: General rules and rules for buildings. European Committee for Standardization. Brussels, 2002.
[2] ACI committee 318. Building code requirements for structural concrete (ACI 318-05) and Commentary (ACI 318R-05). USA, 2005.
[3] ASCE-ACI Committee 426. “The shear strength of reinforced concrete members”. J Struct Div, ASCE, Vol. 99, No. 6, 1973 pp. 1091–187.
[4] ASCE-ACI Committee 445. “Recent approaches to shear design of structural concrete”. J Struct Eng ASCE, Vol. 124, No. 12, 1998, pp. 1375–417.
[5] EHE-08. Instrucción de Hormigón Estructural. España: Publicaciones del Ministerio de Fomento, 2008, Secretaría General Técnica.
[6] GRANDSON, L.A. (2005) "Taylor n-dimensional nets, The analytic equivalence to Neural Nets", University Press of Kentucky.
[7] COLLINS MP, BENTZ EG, SHERWOOD EG, XIE L. “An adequate theory for the shear strength of reinforced concrete structures” En: Morley Simposium on Concrete Plasticity and its Application. University of Cambridge: Cambridge; 2008.
[8] DARWIN C. On the origin of species by means of natural selection or the preservation of favoured races in the struggle for life, Cambridge University Press, 1959.
[9] PÉREZ JL, CLADERA A, RABUÑAL JR, MARTÍNEZ-ABELLA F. “Optimal adjustment of EC-2 shear formulation for concrete elements without web reinforcement using Genetic Programming”. Engineering Structures, Vol. 32, No. 11, 2010, pp. 3452-3466.
[10] PEREZ JL. Metodología para orientar procesos de extracción de conocimiento basados en Computación Evolutiva. Aplicación al desarrollo de modelos y formulaciones en el ámbito del hormigón estructural, Tesis doctoral, Departamento de Tecnologías de la Información y las Comunicaciones, Universidad de A Coruña, 2010.
[11] BENTZ EC. Sectional analysis of reinforced concrete members, Tesis doctoral, Department of Civil Engineering, University of Toronto, 2000.
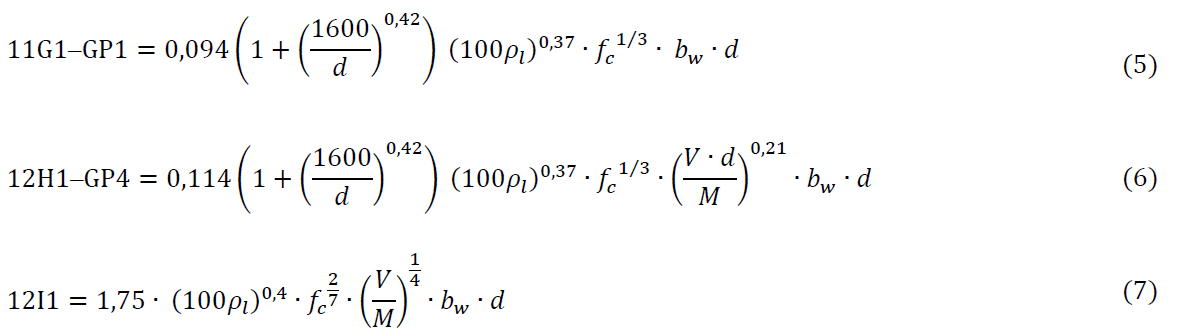


No hay comentarios:
Publicar un comentario